密码学Golang

https://subingwen.cn/golang/cryptology

密码

发送者、接收者、窃听者

请想象一个Alice向Bob发送电子邮件的场景。在这个场景中，发出邮件的Alice称为 发送者（sender），而收到邮件的Bob则称为 接收者（receiver）。

在讲解发送者、接收者的概念时，用邮件这个例子会比较便于理解，但实际上发送者和接收者这两个术语的使用范围并不仅仅局限于邮件。当某个人向另一个人发送信息时，发出信息的人称为发送者，而收到信息的人称为接收者。另外，被发送的信息有时也统称为 消息（message）。

Alice向Bob发送邮件

邮件是通过互联网从Alice的计算机发送到Bob的计算机的。在发送邮件时，邮件会经过许多台计算机和通信设备进行中转，在这个过程中，就存在被恶意窃听者（eavesdropper）偷看到的可能性。

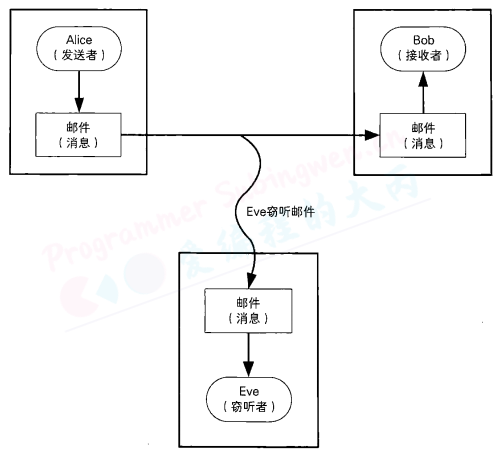
Eve（窃听者）看到邮件的内容

窃听者Eve并不一定是人类，有可能是安装在通信设备上的某种窃听器，也可能是安装在邮件软件和邮件服务器上的某些程序。

尽管邮件内容原本应该只有发送者和接收者两个人知道，但如果不采取相应的对策，就存在被第三方知道的风险。

加密和解密

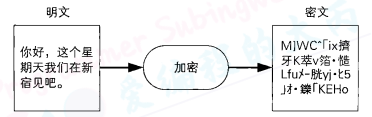
Alice不想让别人看到邮件的内容，于是她决定将邮件进行加密（encrypt）后再发送出去。

加密之前的消息称为明文（plaintext），加密之后的消息称为密文（cipher-text）。

我们看到明文可以理解其中的含义，而看到密文则无法理解其中的含义。

明文加密之后就会变成看不懂的密文

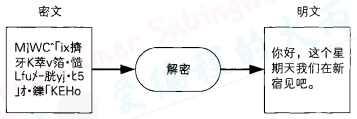
Bob收到了来自Alice的加密邮件，但作为接收者的Bob也是无法直接阅读密文的，于是 Bob需要对密文进行解密（decrypt）之后再阅读。解密就是将密文恢复成明文的过程。

密文解密之后就变成了原来的明文

将消息加密后发送的话，即使消息被窃听，窃听者得到的也只是密文，而无法得知加密前的明文内容

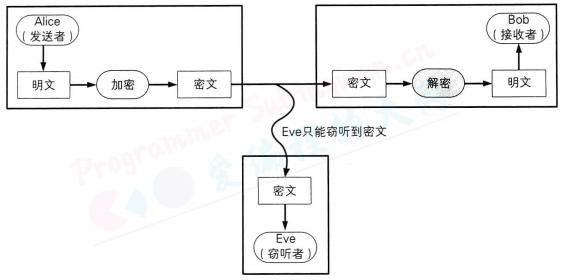
将消息加密后发送, 窃听者只能得到密文

在上述场景中，Alice将邮件进行加密，而Bob则进行解密，这样做的目的，是为了不让窃听者Eve读取邮件的内容Alice和Bob通过运用密码(cryptography)技术， 保证了邮件的机密性（confidentiality）。

密码算法

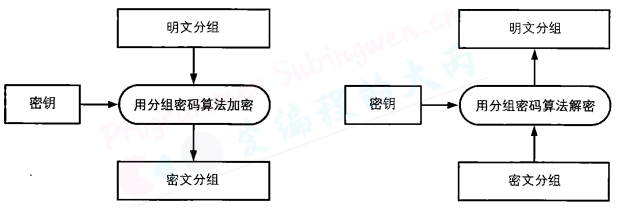
用于解决复杂问题的步骤，通常称为算法（algorithm）。从明文生成密文的步骤，也就是加密的步骤，称为“加密算法”，而解密的步骤则称为“解密算法”。加密、解密的算法合在一起统称为密码算法。

密钥

密码算法中需要密钥（key）。现实世界中的“钥’’，是像 :key: 这样的形状微妙而复杂的小金属片。然而，密码算法中的密钥，则是像203554728568477650354673080689430768这样的一串非常大的数字。

密钥

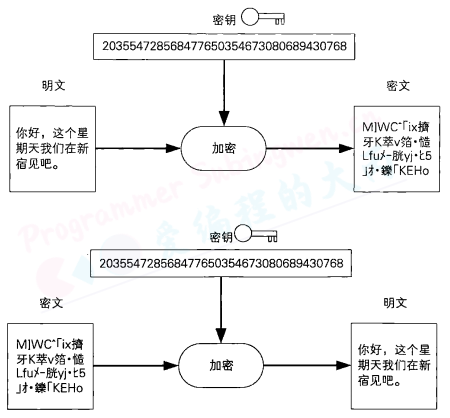
无论是在加密时还是在解密时，都需要知道密钥。

正如保险柜的钥匙可以保护保险柜中存放的贵重物品一样，密码中的密钥可以保护你的重要数据。即使保险箱再坚固，如果钥匙被盗, 里面的贵重物品也会被盗。同样地我们也必须注意不要让密码的密钥被他人窃取。

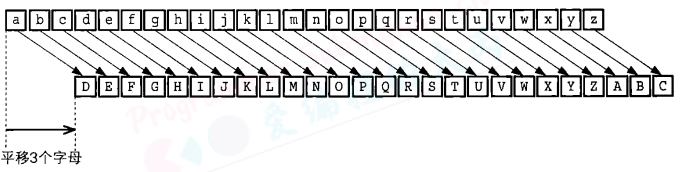
凯撒密码的加密

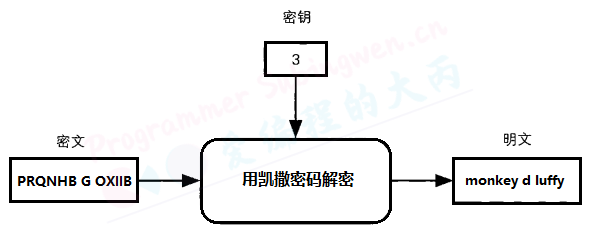
恺撒密码（Caesar cipher）是一种相传尤利乌斯·恺撒曾使用过的密码。恺撒于公元前100年左右诞生于古罗马，是一位著名的军事统帅。

恺撤密码是通过将明文中所使用的字母表按照一定的字数“平移”来进行加密的。比如在日语（例如平假名）或者汉语（例如汉语拼音）或者英文字母表中都可以用同样的思路来实现恺撒密码。

为了讲解方便，我们用小写字母（a，b，c，…）来表小明文，用大写字母（A，B，C，…）来表示密文。

现在我们将字母表平移3个字母，于是，明文中的a在加密后就变成了与其相隔3个字母的D，以此类推。b变成E，c变成F，d变成G……v变成Y，w变成Z，而x则会回到字母表的开头而变成A，相应地，y变成B，z变成C。通过下图我们可以很容易地理解“平移”的具体工作方式。

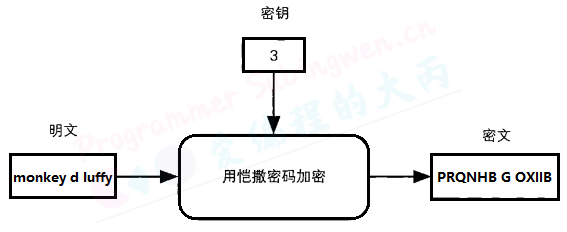
凯撒密码的加密

这里，我们假设要保密的信息为monkey d luffy这个男孩的名字。我们暂且不管这个名字到底代表一位真实的男性，还是只是一种暗号，只考虑将它在保密的状态下发送给接收者。

此时，明文包含下列12个字母：monkey d luffy, 接下来我们对明文中的字母逐一加密:

m   --->    P               
o   --->    R
n   --->    Q
k   --->    N
e   --->    H
y   --->    B
d   --->    G
l   --->    O
u   --->    X
f   --->    I
f   --->    I
y   --->    B

这样，明文 monkey d luffy 就被转换成了密文PRQNHB G OXIIB，monkey d luffy这个词我们能够看懂，但PRQNHB G OXIIB就看不懂了。

恺撒密码中，将字母表中的字母平移这个操作就是密码的算法，而平移的字母数量则相当于密钥。在上面的例子中，密钥为3（如下图）。

凯撒密码的加密

凯撒密码的解密

现在，假设接收者已经收到了密文PRQNHB G OXIIB，由于密文本身是看不懂的，因此必须将它解密成明文。

恺撒密码的解密过程是使用与加密时相同的密钥进行反向的平移操作。用刚才的例子来说，只要反向平移3个字母就可以解密了。

P   --->    m               
R   --->    o
Q   --->    n
N   --->    k
H   --->    e
B   --->    y
G   --->    d
O   --->    l
X   --->    u
I   --->    f
I   --->    f
B   --->    y

这样我们就得到了明文monkey d luffy。

在这个场景中， 秘钥3必须由发送者和接收者事先约定好。

凯撒密码的解密

密码信息安全尝试

  1. 不要使用保密的密码算法
  2. 使用低强度的密码比不进行任何加密更危险
  3. 任何密码总有一天都会被破解
  4. 密码只是信息安全的一部分

不要使用保密的密码算法

很多企业都有下面这样的想法：

“由公司自己开发一种密码算法，并将这种算法保密，这样就能保证安全。然而，这样的想法却是大错特错，使用保密的密码算法是无法获得高安全性的。我们不应该制作或使用任何保密的密码算法，而是应该使用那些已经公开的、被公认为强度较高的密码算法。

这样做的原因主要有以下两点：

密码算法的秘密早晚会公诸于世

从历史上看，密码算法的秘密最终无一例外地都会被暴露出来。例如: RSA公司开发的RC4密码算法曾经也是保密的，但最终还是有一位匿名人士开发并公开了与其等效的程序。

一旦密码算法的详细信息被暴露，依靠对密码算法本身进行保密来确保机密性的密码系统也就土崩瓦解了。反之，那些公开的算法从一开始就没有设想过要保密，因此算法的暴露丝毫不会削弱它们的强度。

开发高强度的密码算法是非常困难的

  1. 要比较密码算法的强弱是极其困难的，因为密码算法的强度并不像数学那样可以进行严密的证明。密码算法的强度只能通过事实来证明，如果专业密码破译者经过数年的尝试仍然没有破解某个密码算法，则说明这种算法的强度较高。

  2. 稍微聪明一点的程序员很容易就能够编写出“自己的密码系统”。这样的密码在外行看来貌似牢不可破，但在专业密码破译者的眼里，要破解这样的密码几乎是手到擒来。

  3. 现在世界上公开的被认为强度较高的密码算法，几乎都是经过密码破译者长期尝试破解未果而存活下来的。因此，如果认为“公司自己开发的密码系统比那些公开的密码系统更强”，那只能说是过于高估自己公司的能力了。

  4. 试图通过对密码算法本身进行保密来确保安全性的行为，一般称为隐蔽式安全性（securitybyobscurity），这种行为是危险且愚蠢的。

  5. 反过来说，将密码算法的详细信息以及程序源代码全部交给专业密码破译者，并且为其提供大量的明文和密文样本，如果在这样的情况下破译一段新的密文依然需要花上相当长的时间，就说明这是高强度的密码。

使用低强度的密码比不进行任何加密更危险

一般人们会认为．就算密码的强度再低，也比完全不加密要强吧？其实这样的想法是非常危险的。

正确的想法应该是：与其使用低强度的密码，还不如从一开始就不使用任何密码这主要是由于用户容易通过“密码”这个词获得一种“错误的安全感”。对于用户来说，安全感与密码的强度无关，而只是由“信息已经被加密了”这一事实产生的，而这通常会导致用户在处理一些机密信息的时候麻痹大意。

任何密码总有一天会被破译

如果某种密码产品宣称“本产品使用了绝对不会被破解的密码算法”，那么你就要对这个产品的安全性打个问号了，这是因为绝对不会被破解的密码是不存在的。

无论使用任何密码算法所生成的密文，只要将所有可能的密钥全部尝试一遍，就总有一天可以破译出来。因此，破译密文所需要花费的时间，与要保密的明文的价值之间的权衡就显得非常重要。

密码只是信息安全的一部分

我们还是回到Alice给Bob发送加密邮件的例子。即便不去破解密码算法，也依然有很多方法能够知道Alice所发送的邮件内容, 例如:

攻击者可以不去试图破译经过加密的邮件，而是转而攻击Alice的电脑以获取加密之前的邮件明文。

上面提到的攻击手段，都与密码的强度毫无关系。要保证良好的安全性，就需要理解“系统”这一概念本身的性质复杂的系统就像一根由无数个环节相连组成的链条，如果用力拉，链条就会从其中最脆弱的环节处断开。因此，系统的强度取决于其中最脆弱的环节的强度。

最脆弱的环节并不是密码，而是人类自己。

密码信息威胁

我们将信息安全所面临的威胁与用来用对这些威胁的密码技术直接的关系用一张图标来表示出来。

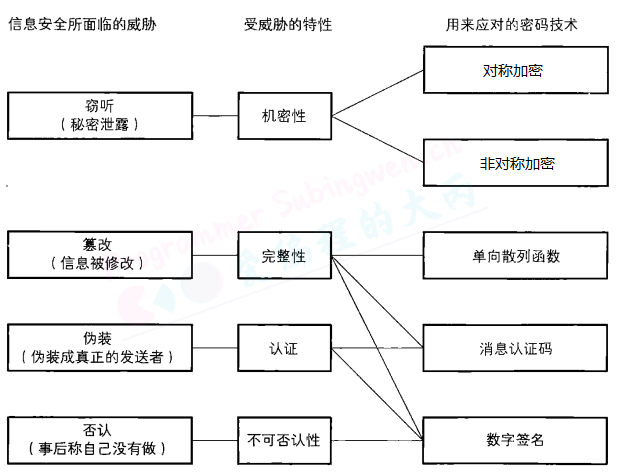
密码信息威胁

对称加密

“对称加密: 也称为对称密码, 是指在加密和解码时使用同一秘钥的加密方式”

对称加密

编码

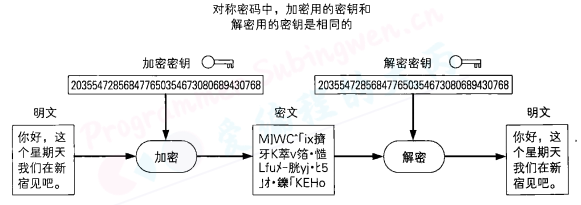
现代的密码都是建立在计算机的基础之上的，这是因为现代的密码所处理的数据量非常大，而且密码算法也非常复杂，不借助计算机的力量就无法完成加密和解密的操作。

计算机的操作对象并不是文字，而是由0和1排列而成的比特序列。无论是文字、图像、声音、视频还是程序，在计算机中都是用比特序列来表示的。执行加密操作的程序，就是将表示明文的比特序列转换为表示密文的比特序列。

将现实世界中的东西映射为比特序列的操作称为编码（encoding）。例如midnight（深夜）这个词，我们可以对其中的每个字母逐一进行编码，这种编码规则叫作ASCII。

编码

注意这里的m –> 01101101这一转换并不是加密而是编码。尽管在人类看来0和1的序列跟密码没什么两样，但计算机却可以“看懂”这些比特序列，并很快地反应出其所对应的字符 midnight

字母m的ASCII编码

什么是DES

DES（Data Encryption Standard） 是1977年美国联邦信息处理标准（FIPS）中所采用的一种对称密码（FIPS46.3）。DES一直以来被美国以及其他国家的政府和银行等广泛使用。然而，随着计算机的进步，现在DES已经能够被暴力破解，强度大不如前了。

RSA公司举办过破泽DES密钥的比赛（DESChallenge），我们可以看一看RSA公司官方公布的比赛结果：

由于DES的密文可以在短时间内被破译，因此除了用它来解密以前的密文以外，现在我们不应该再使用DES了。

DES加密和解密

DES是一种将64比特的明文加密成64比特的密文的对称密码算法，==它的密钥长度是56比特==。尽管 从规格上来说，DES的密钥长度是64比特，但由于每隔7比特会设置一个用于错误检查的比特，因此实质上其密钥长度是56比特。

DES是以64比特的明文（比特序列）为一个单位来进行加密的，这个64比特的单位称为分组。一般来说，以分组为单位进行处理的密码算法称为分组密码（blockcipher），DES就是分组密码的一种。

DES每次只能加密64比特的数据，如果要加密的明文比较长，就需要对DES加密进行迭代（反复），而迭代的具体方式就称为模式（mode）。

密钥长度(56bit + 8bit)/8 = 8 byte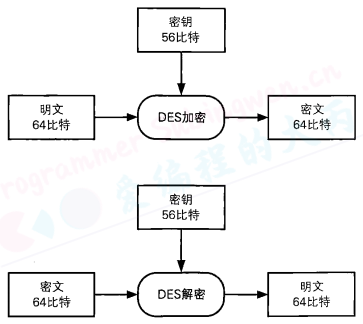
DESC的加密与解密

Go中对DES的操作

在Go中使用DESC需要导入的包

package main // 定义主包，程序可执行

import (
    "bytes"         // 用于处理字节切片
    "crypto/cipher" // 提供加密模式接口，如 CBC
    "crypto/des"   // 提供 DES 加密算法
    "encoding/base64" // 用于 Base64 编码
    "fmt"          // 用于格式化输出
)

// PKCS5Padding 为数据添加 PKCS5 填充，使其长度为块大小的倍数
func PKCS5Padding(ciphertext []byte, blockSize int) []byte {
    // 1. 计算最后一个分组缺少的字节数
    padding := blockSize - (len(ciphertext) % blockSize)
    // 2. 创建一个大小为 padding 的切片，每个字节的值为 padding
    padText := bytes.Repeat([]byte{byte(padding)}, padding)
    // 3. 将填充数据追加到原始数据后
    newText := append(ciphertext, padText...)
    return newText
}

// PKCS5UnPadding 移除数据尾部的 PKCS5 填充
func PKCS5UnPadding(origData []byte) []byte {
    // 1. 获取数据的总长度
    length := len(origData)
    if length == 0 {
        return origData // 空数据直接返回
    }
    // 2. 获取填充的字节数（最后一个字节表示填充数量）
    number := int(origData[length-1])
    if number > length || number == 0 {
        return origData // 无效填充，直接返回
    }
    // 3. 移除尾部填充的字节
    return origData[:(length - number)]
}

// DesEncrypt_CBC 使用 DES 算法在 CBC 模式下加密数据
func DesEncrypt_CBC(src, key []byte) []byte {
    // 创建 DES 加密器
    block, err := des.NewCipher(key)
    if err != nil {
        panic(err) // 错误处理（生产环境中应返回错误）
    }
    // 对输入数据进行 PKCS5 填充
    src = PKCS5Padding(src, block.BlockSize())
    // 定义初始化向量（IV），长度需为 8 字节
    tmp := []byte("helloAAA")
    // 创建 CBC 模式加密器
    blackMode := cipher.NewCBCEncrypter(block, tmp)
    // 创建输出缓冲区
    dst := make([]byte, len(src))
    // 执行加密操作
    blackMode.CryptBlocks(dst, src)

    fmt.Println("加密之后的数据: ", dst)
    return dst
}

// DesDecrypt_CBC 使用 DES 算法在 CBC 模式下解密数据
func DesDecrypt_CBC(src, key []byte) []byte {
    // 创建 DES 解密器
    block, err := des.NewCipher(key)
    if err != nil {
        panic(err) // 错误处理（生产环境中应返回错误）
    }

    // 定义初始化向量（IV），与加密时相同
    tmp := []byte("helloAAA")
    // 创建 CBC 模式解密器
    blockMode := cipher.NewCBCDecrypter(block, tmp)

    // 创建新的输出缓冲区，避免修改输入数据
    dst := make([]byte, len(src))
    // 执行解密操作
    blockMode.CryptBlocks(dst, src)

    // 移除 PKCS5 填充
    dst = PKCS5UnPadding(dst)

    return dst
}

// DESText 测试 DES 加密和解密功能
func DESText() {
    // 定义 8 字节密钥
    key := []byte("11111111")
    // 待加密的中文文本
    plaintext := []byte("床前明月光, 疑是地上霜. 举头望明月, 低头思故乡.")
    // 执行加密
    result := DesEncrypt_CBC(plaintext, key)
    // 输出 Base64 编码的加密数据
    fmt.Println("Base64 编码的加密数据: ", base64.StdEncoding.EncodeToString(result))
    // 执行解密
    result = DesDecrypt_CBC(result, key)
    // 输出解密后的文本
    fmt.Println("解密之后的数据: ", string(result))
}

// main 程序入口
func main() {
    DESText()
}

安全性问题：

  1. DES 算法已过时，密钥长度（56 位）不适合现代安全需求，建议使用 AES。
  2. 固定的 IV（helloAAA）不安全，实际应用中应为每次加密生成随机 IV。
  3. 硬编码密钥（11111111）不安全，应使用安全的密钥管理机制

背景知识

  1. DES 块大小：DES 算法的块大小是 8 字节。加密时，输入数据（明文）必须是 8 字节的整数倍。如果不是，必须通过填充（padding）来补齐。
  2. PKCS5 填充：PKCS5 填充（严格来说是 PKCS7 填充的子集，适用于 8 字节块大小）会确保数据长度是块大小的倍数，即使明文长度已经满足要求，也会添加额外的填充块。
  3. 解密时的处理：解密后，PKCS5UnPadding 函数会移除填充，恢复原始明文。

初始化向量的作用

初始化向量（IV）是一个固定长度的随机或伪随机数据块，与密钥一起用于加密和解密过程。它的主要作用包括：

  1. 增加加密的安全性：
  2. 打破块加密的确定性：
  3. 支持链式加密：
  4. 解密时同步：

CBC 模式的加密和解密过程如下：

加密：

  1. 明文被分成 8 字节的块（对于 DES）。
  2. 第一个明文块与 IV 异或，然后用密钥加密生成第一个密文块。
  3. 后续每个明文块与前一个密文块异或，再用密钥加密。
  4. 最终密文由所有密文块组成。

解密：

  1. 第一个密文块用密钥解密后，与 IV 异或，得到第一个明文块。
  2. 后续每个密文块解密后，与前一个密文块异或，得到对应的明文块。
  3. 移除 PKCS5 填充（如果有），恢复原始明文。

IV 的作用是作为链的起点，确保加密的随机性和安全性。

三重DES的加密

现在DES已经可以在现实的时间内被暴力破解，因此我们需要一种用来替代DES的分组密码，三重DES就是出于这个目的被开发出来的。

三重DES（triple-DES）

是为了增加DES的强度，==将DES重复3次所得到的一种密码算法==，通常缩写为3DES。

三重 DES 的工作原理

三重 DES 使用 三个 DES 密钥（总长度通常为 112 位或 168 位），对数据进行三次 DES 操作，分为加密（Encrypt）、解密（Decrypt）和再次加密（Encrypt），即 EDE 模式（Encrypt-Decrypt-Encrypt）。具体流程如下：

为什么中间是解密？

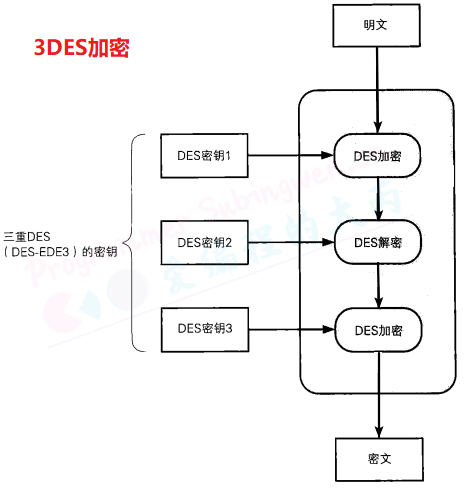
3DES加密
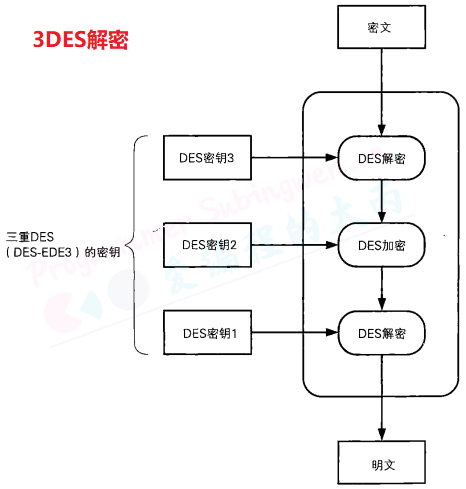
3DES解密

明文经过三次DES处理才能变成最后的密文，由于DES密钥的长度实质上是56比特，因此三重DES的密钥长度就是56×3=168比特, 加上用于错误检测的标志位8x3（奇偶校验）, 共192bit。

Go中对3DES的操作

下面为用Go实现的3DES样例

package main

import (
    "bytes"
    "crypto/cipher"
    "crypto/des"
    "crypto/rand"
    "encoding/base64"
    "fmt"
)

// PKCS5Padding 为数据添加 PKCS5 填充，使其长度为块大小的倍数
func PKCS5Padding(ciphertext []byte, blockSize int) []byte {
    padding := blockSize - (len(ciphertext) % blockSize)
    padText := bytes.Repeat([]byte{byte(padding)}, padding)
    return append(ciphertext, padText...)
}

// PKCS5UnPadding 移除数据尾部的 PKCS5 填充
func PKCS5UnPadding(origData []byte) []byte {
    length := len(origData)
    if length == 0 {
        return origData
    }
    number := int(origData[length-1])
    if number > length || number == 0 {
        return origData // 无效填充，返回原数据
    }
    return origData[:(length - number)]
}

// TripleDESEncrypt 使用三重 DES 在 CBC 模式下加密数据，返回密文和 IV
func TripleDESEncrypt(src, key []byte) ([]byte, []byte, error) {
    // 创建三重 DES 加密器（密钥长度需为 16 或 24 字节）
    block, err := des.NewTripleDESCipher(key)
    if err != nil {
        return nil, nil, fmt.Errorf("创建三重 DES 加密器失败: %v", err)
    }

    // 生成随机 IV（8 字节，与块大小一致）
    iv := make([]byte, block.BlockSize())
    if _, err := rand.Read(iv); err != nil {
        return nil, nil, fmt.Errorf("生成随机 IV 失败: %v", err)
    }

    // 填充明文
    src = PKCS5Padding(src, block.BlockSize())
    // 创建 CBC 模式加密器
    mode := cipher.NewCBCEncrypter(block, iv)
    // 创建输出缓冲区
    dst := make([]byte, len(src))
    // 执行加密
    mode.CryptBlocks(dst, src)

    fmt.Println("加密后的数据: ", dst)
    return dst, iv, nil
}

// TripleDESDecrypt 使用三重 DES 在 CBC 模式下解密数据
func TripleDESDecrypt(src, key, iv []byte) ([]byte, error) {
    // 创建三重 DES 解密器
    block, err := des.NewTripleDESCipher(key)
    if err != nil {
        return nil, fmt.Errorf("创建三重 DES 解密器失败: %v", err)
    }

    // 创建 CBC 模式解密器
    mode := cipher.NewCBCDecrypter(block, iv)
    // 创建输出缓冲区
    dst := make([]byte, len(src))
    // 执行解密
    mode.CryptBlocks(dst, src)

    // 移除 PKCS5 填充
    dst = PKCS5UnPadding(dst)
    return dst, nil
}

// TripleDESText 测试三重 DES 加密和解密
func TripleDESText() error {
    // 使用 24 字节密钥（3密钥模式）
    key := []byte("123456789012345612345678")
    plaintext := []byte("床前明月光, 疑是地上霜. 举头望明月, 低头思故乡.")

    // 加密
    ciphertext, iv, err := TripleDESEncrypt(plaintext, key)
    if err != nil {
        return fmt.Errorf("加密失败: %v", err)
    }
    fmt.Println("Base64 编码的加密数据: ", base64.StdEncoding.EncodeToString(ciphertext))
    fmt.Println("使用的 IV: ", iv)

    // 解密
    result, err := TripleDESDecrypt(ciphertext, key, iv)
    if err != nil {
        return fmt.Errorf("解密失败: %v", err)
    }
    fmt.Println("解密后的数据: ", string(result))
    return nil
}

func main() {
    if err := TripleDESText(); err != nil {
        fmt.Println("错误: ", err)
    }
}

AES（Advanced Encryption Standard）

AES（Advanced Encryption Standard）是取代其前任标准（DES）而成为新标准的一种对称密码算法。全世界的企业和密码学家提交了多个对称密码算法作为AES的候选，最终在2000年从这些候选算法中选出了一种名为 Rijndael 的对称密码算法，并将其确定为了AES。

Rijndael 是由比利时密码学家 Joan Daemen 和 Vincent Rijmen 设汁的分组密码算法，今后会有越来越多的密码软件支持这种算法。

Rijndael的分组长度为128比特，密钥长度可以以32比特为单位在128比特到256比特的范围内进行选择（不过在AES的规格中，密钥长度只有128、192和256比特三种）。

128bit=16byte
192bit=24byte
256bit=32byte

在go提供的接口中密钥长度只能是16字节。

AES的加密和解密

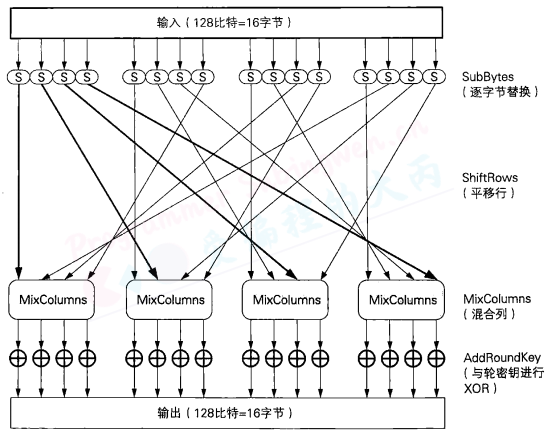
和DES—样，AES算法也是由多个轮所构成的，下图展示了每一轮的大致计算步骤。DES使用Feistel网络作为其基本结构，而AES没有使用Feistel网络，而是使用了SPN Rijndael的输人分组为128比特，也就是16字节。首先，需要逐个字节地对16字节的输入数据进行SubBytes处理。所谓SubBytes,就是以每个字节的值（0～255中的任意值）为索引，从一张拥有256个值的替换表（S-Box）中查找出对应值的处理，也是说，将一个1字节的值替换成另一个1字节的值。

SubBytes之后需要进行ShiftRows处理，即将SubBytes的输出以字节为单位进行打乱处理。从下图的线我们可以看出，这种打乱处理是有规律的。

ShiftRows之后需要进行MixCo1umns处理，即对一个4字节的值进行比特运算，将其变为另外一个4字节值。

最后，需要将MixColumns的输出与轮密钥进行XOR，即进行AddRoundKey处理。到这里，AES的一轮就结東了。实际上，在AES中需要重复进行10 ~ 14轮计算。

通过上面的结构我们可以发现输入的所有比特在一轮中都会被加密。和每一轮都只加密一半输人的比特的Feistel网络相比，这种方式的优势在于加密所需要的轮数更少。此外，这种方式还有一个优势，即SubBytes，ShiftRows和MixColumns可以分别按字节、行和列为单位进行并行计算。

AES加密

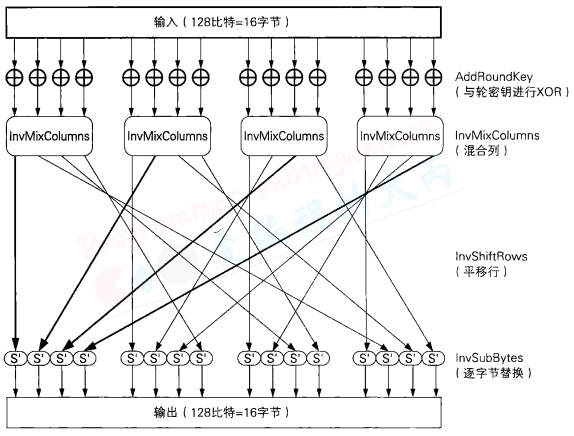
下图展示了AES中一轮的解密过程。从图中我们可以看出，SubBytes、ShiftRows、MixColumns分别存在反向运算InvSubBytes、InvShiftRows、InvMixColumns，这是因为AES不像Feistel网络一样能够用同一种结构实现加密和解密。

AES解密

Go中对AES的使用

加解密实现思路

加密-CBC分组模式

  1. 创建返回一个使用AES算法的cipher.Block接口
  1. 对最后一个明文分组进行数据填充
  1. 创建一个密码分组为链接模式的, 底层使用AES加密的BlockMode接口
  2. 加密连续的数据块

解密

  1. 创建并返回一个使用AES算法的cipher.Block接口
  2. 创建一个密码分组为链接模式的, 底层使用AES解密的BlockMode接口
  3. 数据块解密
  4. 去掉最后一组的填充数据

AES加密解密代码

package main

import (
    "bytes"
    "crypto/aes"
    "crypto/cipher"
    "fmt"
)

// PKCS5Padding 为数据添加 PKCS5 填充，使其长度为块大小的倍数
func PKCS5Padding(ciphertext []byte, blockSize int) []byte {
    padding := blockSize - (len(ciphertext) % blockSize)
    padText := bytes.Repeat([]byte{byte(padding)}, padding)
    return append(ciphertext, padText...)
}

// PKCS5UnPadding 移除数据尾部的 PKCS5 填充
func PKCS5UnPadding(origData []byte) []byte {
    length := len(origData)
    if length == 0 {
        return origData
    }
    number := int(origData[length-1])
    if number > length || number == 0 {
        return origData // 无效填充，返回原数据
    }
    return origData[:(length - number)]
}

// AES加密实现
func AESEncrypt(src, key []byte) []byte {
    // 1. 创建一个使用AES加密的块对象
    block, err := aes.NewCipher(key)
    if err != nil {
        panic(err)
    }
    // 2. 最后一个分组进行数据填充
    src = PKCS5Padding(src, block.BlockSize())
    // 3. 创建一个分组为链接模式，底层使用AES加密的块模型对象
    blockMode := cipher.NewCBCEncrypter(block, key[:block.BlockSize()])
    // 4.加密
    dst := src
    blockMode.CryptBlocks(dst, src)
    return dst
}

// AES解密
func AESDecrypt(src, key []byte) []byte {
    // 1.创建一个使用AES解密的块对象
    block, err := aes.NewCipher(key)
    if err != nil {
        panic(err)
    }
    // 2. 创建分组为链接模式，底层使用AES的解密模型对象
    blockMode := cipher.NewCBCDecrypter(block, key[:block.BlockSize()])
    // 3. 解密
    dst := src
    blockMode.CryptBlocks(dst, src)
    // 4. 去掉尾部填充的字
    dst = PKCS5UnPadding(dst)
    return dst
}

func main() {
    // 16bytes
    key := "qpwoeirutyalskdj"
    src := "高浓度发v佛为京东文件发你"
    encrypt := string(AESEncrypt([]byte(src), []byte(key)))
    fmt.Println(encrypt)
    fmt.Println(string(AESDecrypt([]byte(encrypt), []byte(key))))
}

应选择哪种对称加密

前面我们介绍了DES、三重DES和AES等对称密码，那么我们到底应该使用哪一种对称密码算法呢？

  1. 今后最好不要将DES用于新的用途，因为随着计算机技术的进步，现在用暴力破解法已经能够在现实的时间内完成对DES的破译。但是，在某些情况下也需要保持与旧版本软件的兼容性。
  2. 出于兼容性的因素三重DES在今后还会使用一段时间，但会逐渐被AES所取代。
  3. 今后大家应该使用的算法是AES（Rijndael），因为它安全、快速，而且能够在各种平台上工作。此外，由于全世界的密码学家都在对AES进行不断的验证，因此即便万一发现它有什么缺陷，也会立刻告知全世界并修复这些缺陷。

一般来说，我们不应该使用任何自制的密码算法，而是应该使用AES。因为AES在其选定过程中，经过了全世界密码学家所进行的高品质的验证工作，而对于自制的密码算法则很难进行这样的验证。

分组密码的模式

"分组密码的模式 -- 分组密码是如何迭代的"

上面介绍的DES和AES都属于分组密码，它们只能加密固定长度的明文。如果需要加密任意长度的明文，就需要对分组密码进行迭代，而分组密码的迭代方法就称为分组密码的“模式”。

分组密码有很多种模式，如果模式的选择不恰当，就无法保证机密性。例如，如果使用ECB模式，明文中的一些规律就可以通过密文被识别出来。

分组密码的主要模式(ECB、CBC、CFB、OFB、CTR)。

分组密码

分组密码（blockcipher） 是每次只能处理特定长度的一块数据的一类密码算法，这里的一块”就称为 分组（block） 。此外，一个分组的比特数就称为 分组长度（blocklength）。

例如，DES和三重DES的分组长度都是64比特。这些密码算法一次只能加密64比特的明文．并生成64比特的密文。

AES的分组长度可以从128比特、192比特和256比特中进行选择。当选择128比特的分组长度时，AES一次可加密128比特的明文，并生成128比特的密文。

分组密码的模式

分组密码算法只能加密固定长度的分组，但是我们需要加密的明文长度可能会超过分组密码的分组长度，这时就需要对分组密码算法进行迭代，以便将一段很长的明文全部加密。而迭代的方法就称为分组密码的模式（mode）。

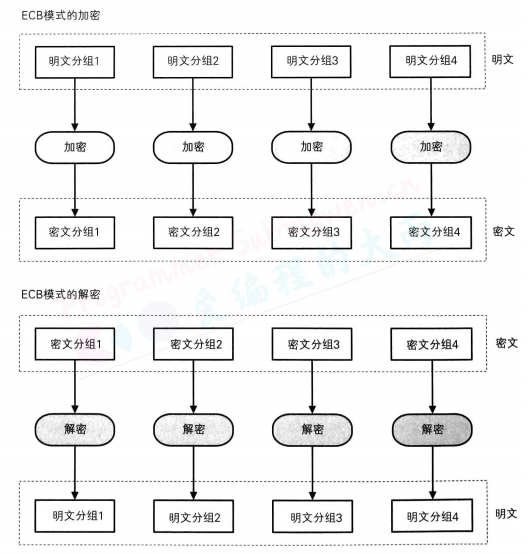
话说到这里，很多读者可能会说：“如果明文很长的话，将明文分割成若干个分组再逐个加密不就好了吗？”事实上可没有那么简单。将明文分割成多个分组并逐个加密的方法称为 ECB模式，这种模式具有很大的弱点（稍后讲解）。对密码不是很了解的程序员在编写加密软件时经常会使用ECB模式，但这样做会在不经意间产生安全漏洞，因此大家要记住千万不能使用ECB模式。

模式有很多种类，分组密码的主要模式有一下5种：

明文分组和密文分组

明文分组和密文分组

ECB模式

ECB(Electronic Code Book, 电子密码本)模式 是最简单的加密模式，明文消息被分成固定大小的块（分组），并且每个块被单独加密。 每个块的加密和解密都是独立的，且使用相同的方法进行加密，所以可以进行并行计算，但是这种方法一旦有一个块被破解，使用相同的方法可以解密所有的明文数据，安全性比较差。 适用于数据较少的情形，加密前需要把明文数据填充到块大小的整倍数。

ECB模式 
                     Key
Plaintext->block cipher encryption->Ciphertext
                     Key
Ciphertext->block cipher decryption->Plaintext

使用ECB模式加密时，相同的明文分组会被转换为相同的密文分组，也就是说，我们可以将其理解为是一个巨大的“明文分组–>密文分组”的对应表，因此ECB模式也称为电子密码本模式当最后一个明文分组的内容小于分组长度时，需要用一特定的数据进行填充（padding），让值一个分组长度等于分组长度。

ECB模式是所有模式中最简单的一种。ECB模式中，明文分组与密文分组是一一对应的关系，因此，如果明文中存在多个相同的明文分组，则这些明文分组最终都将被转换为相同的密文分组。这样一来，只要观察一下密文，就可以知道明文中存在怎样的重复组合，并可以以此为线索来破译密码，因此ECB模式是存在一定风险的。

XOR

XOR的全称是exclusive or,在中文里叫作 异或。

0 XOR 0 = 0
0 XOR 1 = 1
0 XOR 0 = 1
1 XOR 1 = 1

如果将0理解为偶数， 1理解为奇数，就可以将XOR和一般的加法运算等同起来。

偶数 0 + 偶数 0 = 偶数 0
偶数 0 + 奇数 1 = 奇数 1
偶数 0 + 偶数 0 = 奇数 1
奇数 1 + 奇数 1 = 奇数 1

由于XOR和加法运算很相似，因此一般用+和O组合而成的符号⊕来表示XOR。

0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
1 ⊕ 1 = 0

明文为A,密钥为B,只要选择一个合适的B，仅仅使用XOR就可以实现一个高强度的密码。

对同一个比特序列进行两次XOR之后就会回到最初的状态。

CBC模式

CBC(Cipher Block Chaining, 密码块链)模式 中每一个分组要先和前一个分组加密后的数据进行XOR异或操作，然后再进行加密。 这样每个密文块依赖该块之前的所有明文块，为了保持每条消息都具有唯一性，第一个数据块进行加密之前需要用初始化向量IV进行异或操作。 CBC模式是一种最常用的加密模式，它主要缺点是加密是连续的，不能并行处理，并且与ECB一样消息块必须填充到块大小的整倍数。

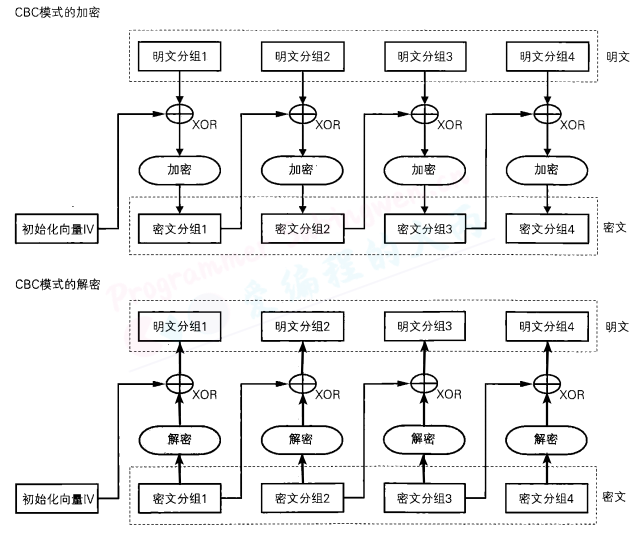
CBC模式

CBC初始化向量

当加密第一个明文分组时，由于不存在“前一个密文分组”，因此需要事先准备一个长度为一个分组的比特序列来代替“前一个密文分组“，这个比特序列称为 初始化向量（initialization vector） 。

通常缩写为 IV 一般来说，每次加密时都会随机产生一个不同的比特序列来作为初始化向量。

明文分组在加密之前一定会与“前一个密文分组”进行 XOR 运算，因此即便明文分组1和2的值是相等的，密文分组1和2的值也不一定是相等的。这样一来，ECB模式的缺陷在CBC模式中就不存在了。

CFB模式

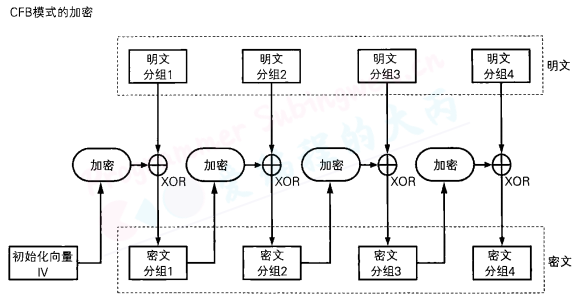
CFB模式的全称是Cipher FeedBack模式（密文反馈模式）。在CFB模式中，前一个分组的密文加密后和当前分组的明文XOR异或操作生成当前分组的密文。

所谓反馈，这里指的就是返回输人端的意思，即前一个密文分组会被送回到密码算法的输入端。

CFB模式的加密：由前一组的密文与下一组明文异或生成下一组的密文。

CFB模式的加密

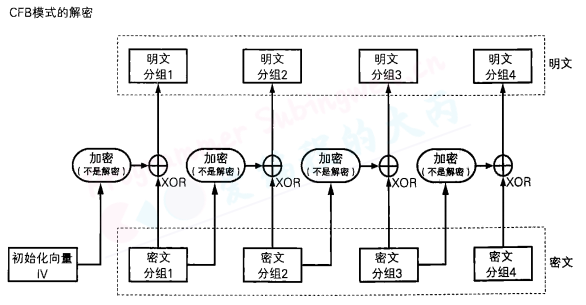
CFB模式的解密：

CFB模式的解密

在ECB模式和CBC模式中，明文分组都是通过密码进行加密的，然而，在CFB模式中，明文分组并没有通过密码算法来直接进行加密。

在CFB模式中，明文分组和密文分组之间并没有经过”加密”这一步骤。明文分和密文分组之间只有一个XOR。

CFB初始化向量

在生成第一个密文分组时，由于不存在前一个输出的数据，因此需要使用初始化向量（IV）来代替，这一点和CBC模式是相同的。一般来说，我们需要在每次加密时生成一个不同的随机比特序列用作初始化向量。

CFB模式与流密码

CFB模式是通过将“明文分组”与“密码算法的输出”进行XOR运算来生成“密文分组”的。

在CFB模式中，密码算法的输出相当于一个随机比特序列。由于密码算法的输出是通过计算得到的，并不是真正的随机数，因此CFB模式不可能具各理论上不可破译的性质。

CFB模式中由密算法所生成的比特序列称为密钥流（key stream）。在CFB模式中，密码算法就相当于用来生成密钥流的伪随机数生成器，而初始化向量相当于伪随机数生成器的“种子“。

在CFB模式中，明文数据可以被逐比特加密，因此我们可以将CFB模式看做是一种使用分组密码来实现流密码的方式。

OFB模式

OFB式的全称是Output-Feedback模式（输出反馈模式）。在OFB模式中，密码算法的输出会反馈到密码算法的输入中， 即上一个分组密码算法的输出是当前分组密码算法的输入。

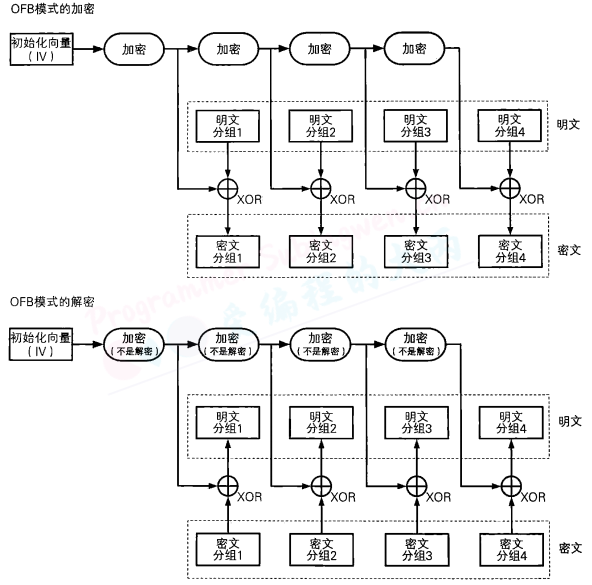
OFB模式加密与解密

OFB模式初始化向量

和CBC模式、CFB模式一样，OFB模式中也需要使用初始化向量（IV）。一般来说，我们需要在每次加密时生成一个不同的随机比特序列用作初始化向量。

CFB模式和OFB模式对比

由于CFB模式中是对密文分组进行反馈的，因此必须从第一个明文分组开始按顺序进行加密，也就是说无法跳过明文分组1而先对明文分组2进行加密。

相对地，在OFB模式中，XOR所需要的比特序列（密钥流）可以事先通过密码算法生成，和明文分组无关。只要提前准备好所需的密钥流，则在实际从明文生成密文的过程中，就完全不需要动用密码算法了。只要将明文与密钥流进行XOR就可以了。和AES等密码算法相比，XOR运算的速度是非常快的。这就意味着只要提前准备好密钥流就可以快速完成加密。换个角度来看，生成密钥流的操作和进行XOR运算的操作是可以并行的。

CTR模式

CTR模式的全称是CounTeR模式（计数器模式）。CTR摸式是一种通过将逐次累加的计数器进行加密来生成密钥流的流密码。

CTR模式中，每个分组对应一个逐次累加的计数器，并通过对计数器进行加密来生成密钥流。也就是说，最终的密文分组是通过将计数器加密得到的比特序列，与明文分组进行XOR而得到的。

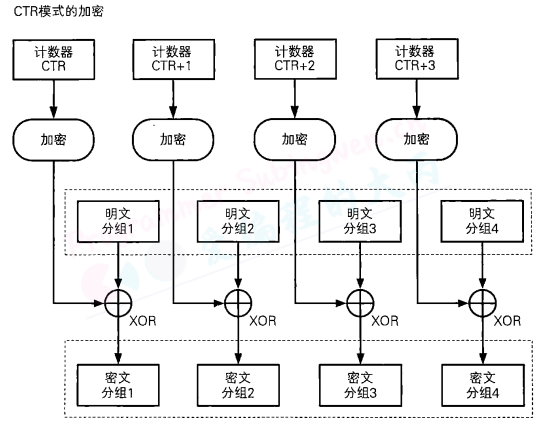
CTR模式的加密
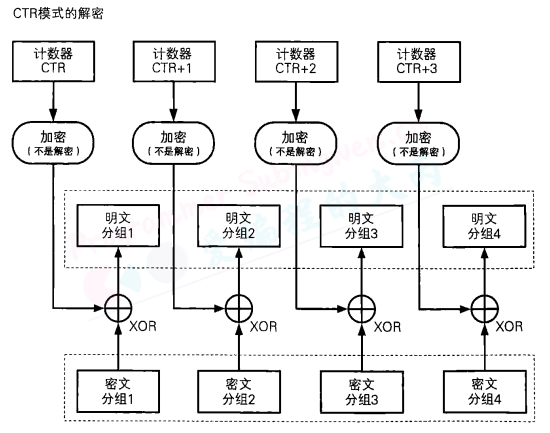
CTR模式的解密

CTR模式计数器的生成方法

每次加密时都会生成一个不同的值（nonce）来作为计数器的初始值。当分组长度为128比特（16字节）时，计数器的初始值可能是像下面这样的形式。

CTR模式计数器的生成方法

其中前8个字节为nonce（随机数），这个值在每次加密时必须都是不同的，后8个字节为分组序号，这个部分是会逐次累加的。在加密的过程中，计数器的值会产生如下变化：

CTR模式计数器计数过程

按照上述生成方法，可以保证计数器的值每次都不同。由于计数器的值每次都不同，因此每个分组中将计数器进行加密所得到的密钥流也是不同的。也是说，这种方法就是用分组密码来模拟生成随机的比特序列。

CTR模式的特点

CTR模式中可以以任意顺序对分组进行加密和解密，因此在加密和解密时需要用到的“计数器”的值可以由nonce和分组序号直接计算出来。这一性质是OFB模式所不具备的。

能够以任意顺序处理分组，就意味着能够实现并行计算。在支持并行计算的系统中，CTR模式的速度是非常快的。

分组密码总结

我们已经介绍了ECB、CBC、CFB、OFB和CTR模式，下面我们对这些模式的特点做一下整理。

分组密码总结

非对称加密

“非对称加密也叫公钥密码: 使用公钥加密, 使用私钥解密”

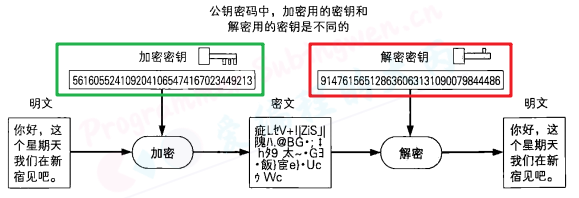
非对称加密

思考一下加密密钥和解密密钥的区别，我们可以发现：

也就是说，解密密钥从一开始就是由接收者自己保管的，因此只要将加密密钥发给发送者就可以解决密钥配送问题了，而根本不需要配送解密密钥。

非对称加密中，加密密钥一般是公开的。正是由于加密密钥可以任意公开，因此该密钥被称为 公钥（publickey）。公钥可以通过邮件直接发送给接收者，也可以刊登在报纸的广告栏上，做成看板放在街上，或者做成网页公开给世界上任何人，而完全不必担心被窃听者窃取。

当然，我们也没有必要非要将公钥公开给全世界所有的人，但至少我们需要将公钥发送给需要使用公钥进行加密的通信对象（也就是给自己发送密文的发送者）。

相对地，解密密钥是绝对不能公开的，这个密钥只能由你自己来使用，因此称为 私钥（privatekey）。私钥不可以被别人知道，也不可以将它发送给别人，甚至也不能发送给自己的通信对象。

公钥和私钥是一一对应的，一对公钥和私钥统称为密钥对（keypair）。由公钥进行加密的密文，必须使用与该公钥配对的私钥才能够解密。密钥对中的两个密钥之间具有非常密切的关系(数学上的关系)一一因此公钥和私钥是不能分别单独生成的。

公钥密码的使用者需要生成一个包括公钥和私钥的密钥对，其中公钥会被发送给别人，而私钥则仅供自己使用。稍后我们将具体尝试生成一个密钥对。

非对称加密通信流程

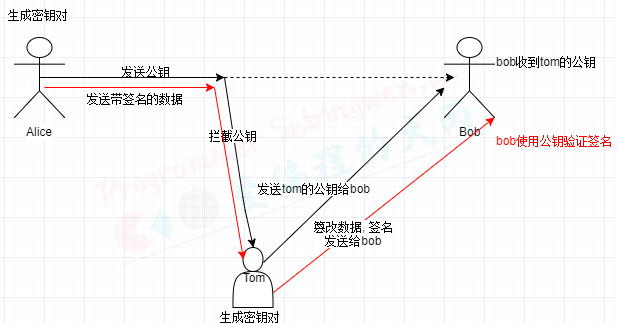
下面我们来看一看使用公钥密码的通信流程。和以前一样、我们还是假设Alice要给Bob发送一条消息，Alice是发送者，Bob是接收者，而这一次窃听者Eve依然能够窃所到他们之间的通信内容。

在公非对称加密通信中，通信过程是由接收者Bob来启动的。

  1. Bob生成一个包含公钥和私钥的密钥对。
  2. Bob将自己的公钥发送给Alicea
  3. Alice用Bob的公钥对消息进行加密。
  4. Alice将密文发送给Bobo
  5. Bob用自己的私钥对密文进行解密。
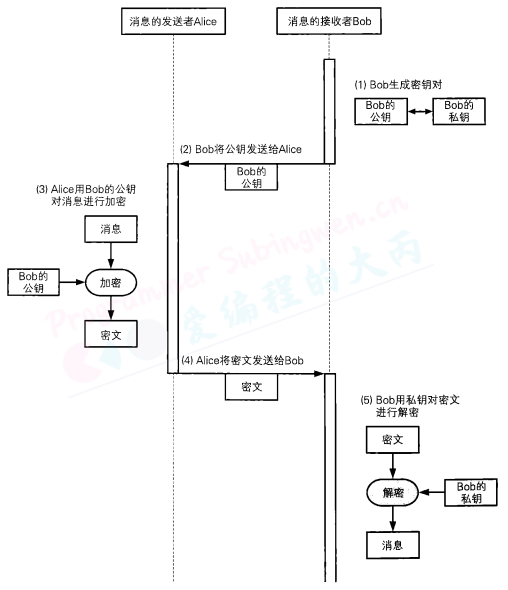
非对称加密通信流程

窃听者Eve可能拥有Bob的公钥，但是Bob的公钥只是加密密钥，而不是解密密钥，因此窃听者Eve就无法完成解密操作。

RSA

非对称加密的密钥分为加密密钥和解密密钥，但这到底是怎样做到的呢？本节中我们来讲解现在使用最广泛的公钥密码算法 RSA。

RSA是一种非对称加密算法，它的名字是由它的三位开发者，即RonRivest、AdiShamir和LeonardAdleman 的姓氏的首字母组成的（Rivest-Shamir-Leonard）。

RSA可以被用于非对称加密和数字签名，关于数字签名我们将在后面章节进行讲解。

1983年，RSA公司为RSA算法在美国取得了专利，但现在该专利已经过期。

RSA加密

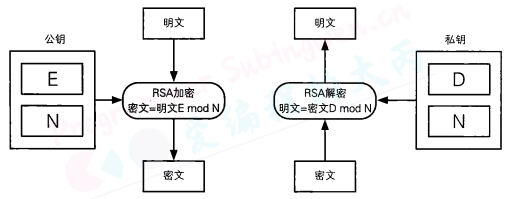
在RSA中，明文、密钥和密文都是数字。RSA的加密过程可以用下列公式来表达，如下。

RSA加密公式

也就是说，RSA的密文是对代表明文的数字的E次方求modN的结果。换句话说，就是将明文自己做E次乘法，然后将其结果除以N求余数，这个余数就是密文。

E和N，到底都是什么数呢？RSA的加密是求明文的E次方modN，因此只要知道E和N这两个数，任何人都可以完成加密的运算。所以说，E和N是RSA加密的密钥，也就是说，E和N的组合就是公钥。

不过，E和N并不是随便什么数都可以的，它们是经过严密计算得出的。顺便说一句，E是加密（Encryption）的首字母，N是数字（Number)的首字母。

RSA解密

RSA的解密和加密一样简单，可以用下面的公式来表达：

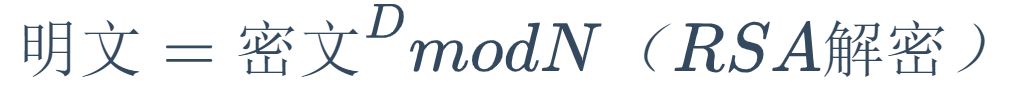
RSA解密公式

对表示密文的数字的D次方求modN就可以得到明文。

这里所使用的数字N和加密时使用的数字N是相同的。数D和数N组合起来就是RSA的解密密钥，因此D和N的组合就是私钥。只有知道D和N两个数的人才能够完成解密的运算。

在RSA中，加密和解密的形式是相同的。加密是求 “E次方的mod N”，而解密则是求 “D次方的modN”

当然，D也并不是随便什么数都可以的，作为解密密钥的D，和数字E有着相当紧密的联系。否则，用E加密的结果可以用D来解密这样的机制是无法实现的。

D是解密〈Decryption）的首字母，N是数字（Number）的首字母。

RSA的加密和解密

Go中生成公钥和私钥

生成私钥操作流程

  1. 使用RSA中的GennerateKey函数生成私钥
  2. 通过x509标准将得到的RSA私钥序列化为ASN.1的DER编码字符串
  3. 将私钥字符串设置到pem格式块中
  4. 通过pem将设置好的数据进行编码，并写入磁盘文件

生成公钥操作流程

  1. 从得到的私钥对象中将公钥信息取出
  2. 通过x509标准将得到的RSA公钥序列化为字符串
  3. 将公钥字符串设置到pem格式块中
  4. 通过pem将设置好的数据进行编码，并写入磁盘文件
package main

import (
    "crypto/rand"
    "crypto/rsa"
    "crypto/x509"
    "encoding/pem"
    "fmt"
    "os"
)

func RSAGenKey(bits int) error {
    // 1. 生成私钥文件
    // GenerateKey函数使用随机数据生成器random生成一对具有指定字位数的RSA密钥
    // 参数1: Reader是一个全局、共享的密码用强随机数生成器
    // 参数2: 秘钥的位数 - bit
    privateKey, err := rsa.GenerateKey(rand.Reader, bits)
    if err != nil {
        return err
    }

    fmt.Println("私钥E: ", privateKey.E)
    fmt.Println("私钥N: ", privateKey.N)

    // 2. MarshalPKCS1PrivateKey将RSA私钥序列化为ASN.1 PKCS#1 DER编码
    derStream := x509.MarshalPKCS1PrivateKey(privateKey)

    // 3. Block代表PEM编码的结构, 对其进行设置
    block := pem.Block{
        Type:  "RSA PRIVATE KEY", //"RSA PRIVATE KEY",
        Bytes: derStream,
    }

    // 4. 创建文件
    privFile, err := os.Create("private.pem")
    if err != nil {
        return err
    }

    defer privFile.Close()

    // 5. 使用pem编码, 并将数据写入文件中
    err = pem.Encode(privFile, &block)
    if err != nil {
        return err
    }

    // 6. 生成公钥文件
    publicKey := privateKey.PublicKey
    fmt.Println("公钥E: ", publicKey.E)
    fmt.Println("公钥N: ", publicKey.N)

    derPkix, err := x509.MarshalPKIXPublicKey(&publicKey)
    if err != nil {
        return err
    }

    block = pem.Block{
        Type:  "RSA PUBLIC KEY", //"PUBLIC KEY",
        Bytes: derPkix,
    }

    pubFile, err := os.Create("public.pem")
    if err != nil {
        return err
    }
    defer pubFile.Close()

    // 7. 编码公钥, 写入文件
    err = pem.Encode(pubFile, &block)
    if err != nil {
        return err
    }

    return nil
}

func main() {
    err := RSAGenKey(256) // 生成256位的RSA密钥对
    if err != nil {
        panic(err)
    }
    os.Exit(0)
}

// 私钥E:  65537
// 私钥N:  85375575361616672744402583273870848398037049301374539680120437284972912763029
// 公钥E:  65537
// 公钥N:  85375575361616672744402583273870848398037049301374539680120437284972912763029

// private.pem
// -----BEGIN RSA PRIVATE KEY-----
// MIGsAgEAAiEAvMDc/H9zxkMdJ3UY/gCLf8PyKh4TO5HQRbI5H6704JUCAwEAAQIh
// AKVkkb8mpvnpQRicAMRBEfnmaMgivNZbFINsIqYpFnbBAhEA6gnKin6te3MgWfG0
// s/qrbQIRAM53NhfjAmdOhY12Jz+AaMkCEQDiAcKOK/bsGClNspSGmbOhAhAahRF7
// q/sJDfr1mrGb5ICRAhEA3/Pu2JLHDHhGIoqSvwE3dQ==
// -----END RSA PRIVATE KEY-----

// public.pem
// -----BEGIN RSA PUBLIC KEY-----
// MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhALzA3Px/c8ZDHSd1GP4Ai3/D8ioeEzuR
// 0EWyOR+u9OCVAgMBAAE=
// -----END RSA PUBLIC KEY-----

Go中使用RSA

公钥加密

  1. 将公钥文件中的公钥读出, 得到使用pem编码的字符串
  2. 将得到的字符串解码
  3. 使用x509将编码之后的公钥解析出来
  4. 使用得到的公钥通过RSA进行数据加密

私钥解密

  1. 将私钥文件中的私钥读出, 得到使用pem编码的字符串
  2. 将得到的字符串解码
  3. 使用x509将编码之后的私钥解析出来
  4. 使用得到的私钥通过RSA进行数据解密
package main

import (
    "crypto/rand"
    "crypto/rsa"
    "crypto/x509"
    "encoding/pem"
    "fmt"
    "os"
)

// RSA公钥加密 明文-> 密文
func RSAEncrypt(src, filename []byte) []byte {
    // 根据文件名将文件内容从文件中读出
    file, err := os.Open(string(filename))
    if err != nil {
        return nil
    }

    defer file.Close()

    // 读文件
    info, _ := file.Stat()
    allText := make([]byte, info.Size())
    file.Read(allText)

    // 从数据中查找到下一个PEM格式的块
    block, _ := pem.Decode(allText)
    if block == nil {
        return nil
    }

    // 解析一个DER编码的公钥
    pubInterface, err := x509.ParsePKIXPublicKey(block.Bytes)
    if err != nil {
        return nil
    }
    pubKey := pubInterface.(*rsa.PublicKey)

    // 公钥加密
    result, _ := rsa.EncryptPKCS1v15(rand.Reader, pubKey, src)
    return result
}

// RSA私钥解密 密文-> 明文
func RSADecrypt(src, filename []byte) []byte {
    // 根据文件名将文件内容从文件中读出
    file, err := os.Open(string(filename))
    if err != nil {
        return nil
    }
    defer file.Close()

    // 读文件
    info, _ := file.Stat()
    allText := make([]byte, info.Size())
    file.Read(allText)

    // 从数据中查找到下一个PEM格式的块
    block, _ := pem.Decode(allText)
    // 解析一个pem格式的私钥
    privateKey, err := x509.ParsePKCS1PrivateKey(block.Bytes)
    // 私钥解密
    result, _ := rsa.DecryptPKCS1v15(rand.Reader, privateKey, src)

    return result
}

func main() {
    encrypted := string(RSAEncrypt([]byte("hello world"), []byte("public.pem")))
    fmt.Println("encrypted:", encrypted)

    plain := RSADecrypt([]byte(encrypted), []byte("private.pem"))
    fmt.Println("plain:", string(plain))

    os.Exit(0)
}

// encrypted: 7&{��~�i�U*w1�A�V������p�8
// plain: hello world

ECC椭圆曲线

椭圆曲线密码学（英语：Elliptic curve cryptography，缩写为 ECC），一种建立公开密钥加密的算法，基于椭圆曲线数学。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。

ECC的主要优势是在某些情况下它比其他的方法使用更小的密钥——比如RSA加密算法——提供相当的或更高等级的安全。

椭圆曲线密码学的许多形式有稍微的不同，所有的都依赖于被广泛承认的解决椭圆曲线离散对数问题的困难性上。与传统的基于大质数因子分解困难性的加密方法不同，ECC通过椭圆曲线方程式的性质产生密钥。

ECC 164位的密钥产生的一个安全级相当于RSA 1024位密钥提供的保密强度，而且计算量较小，处理速度更快，存储空间和传输带宽占用较少。目前我国居民二代身份证正在使用 256 位的椭圆曲线密码，虚拟货币比特币也选择ECC作为加密算法。

数学原理

不管是RSA还是ECC或者其它，公钥加密算法都是依赖于某个正向计算很简单（多项式时间复杂度），而逆向计算很难（指数级时间复杂度）的数学问题。

ECC椭圆曲线详解

公式及图解

y2=x3+ax+by^2 = x^3 + ax + b

其中，aa 和 bb 是曲线参数，满足 4a3+27b2≠04a^3 + 27b^2 \neq 0（确保曲线无奇点）。在有限域（如模 pp 的有限域 FpF_p）上，椭圆曲线由一组满足方程的点和一个无穷远点 OO 组成。 椭圆曲线本身是连续的，应用的是 有限域上的椭圆曲线。加法乘法得到的结果仍然在域内，结果取模达到有限。

关键数学特性：

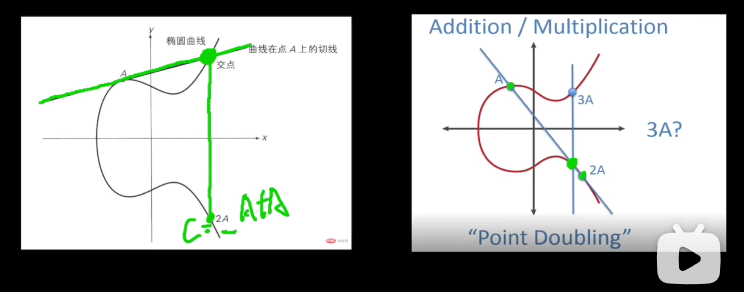
点加法：椭圆曲线上两点 PP 和 QQ 可通过几何方法相加得到新点 R=P+QR = P + Q。 标量乘法：对于点 PP 和整数 kk，计算 Q=kPQ = kP（即 PP 自身加 kk 次）。 离散对数问题：已知 PP 和 Q=kPQ = kP，求解 kk 是非常困难的，这种单向性是ECC安全性的基础。

ECC中的密钥对：

私钥：一个随机大整数 kk。

公钥：通过私钥 kk 和基点 GG（曲线上的一个固定点）计算 Q=kGQ = kG。

ECC椭圆曲线
P+Q计算

ECC生成公钥和私钥的过程

有限域椭圆曲线

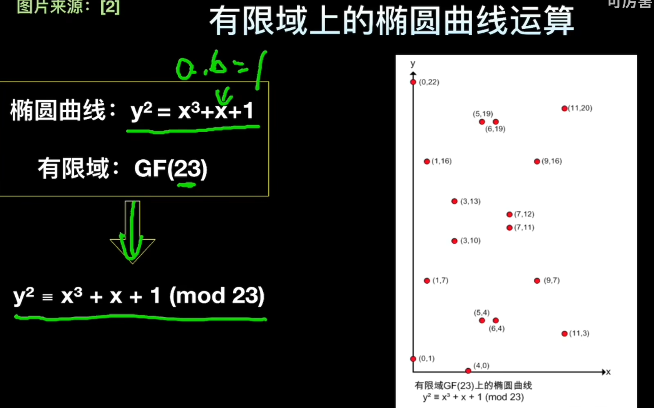
有限域上的椭圆曲线运算

ECC的密钥生成基于椭圆曲线的数学运算，主要涉及点加法和标量乘法。以下是详细步骤：

  1. 选择椭圆曲线和基点
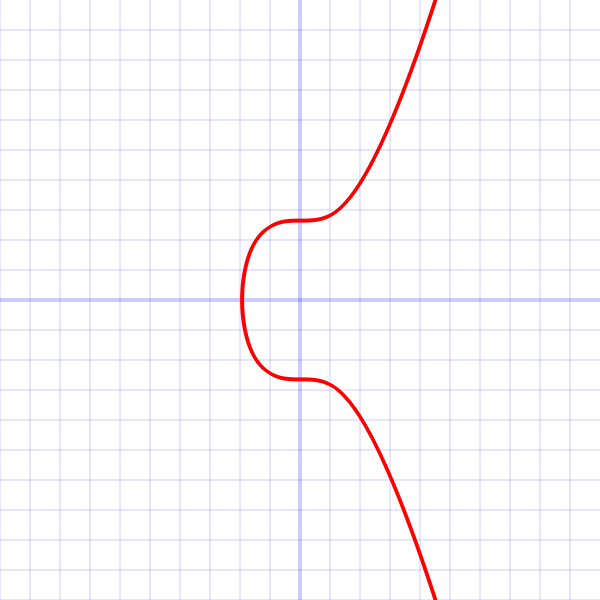
secp256k1

基点 GG 的坐标为一个特定的大整数对。

  1. 生成私钥

私钥 dd 是一个标量（纯数字），没有几何表示。它就像一个“秘密数字”，用于后续计算。

  1. 生成公钥

公钥 QQ：通过计算 Q=dGQ = dG。即，基点 GG 沿着椭圆曲线进行 dd 次点加法运算。 点加法规则（简述）：

若 P=(x1,y1)P = (x_1, y_1)，Q=(x2,y2)Q = (x_2, y_2)，则 P+Q=R=(x3,y3)P + Q = R = (x_3, y_3)，其中：

斜率 m=y2−y1x2−x1modpm = \frac{y_2 - y_1}{x_2 - x_1} \mod p（若 P≠QP \neq Q）。 x3=m2−x1−x2modpx_3 = m^2 - x_1 - x_2 \mod p, y3=m(x1−x3)−y1modpy_3 = m(x_1 - x_3) - y_1 \mod p。

若 P=QP = Q（点自加，倍点），斜率 m=3x12+a2y1modpm = \frac{3x_1^2 + a}{2y_1} \mod p。 若 P=−PP = -P，则 P+(−P)=OP + (-P) = O（无穷远点）。

标量乘法：计算 dGdG 通常使用“双倍-加法”算法（Double-and-Add），将 dd 转换为二进制，结合点加法和倍点高效计算。

例如，d=13=11012d = 13 = 1101_2，则 13G=G+G+4G+8G13G = G + G + 4G + 8G。

计算 2G 由 G算出，3G由 G和2G生成，4G由 2G和2G生成。

椭圆曲线Q=dG计算
有限域上的椭圆曲线运算

分数取模计算方法

1/2 mod 23
n = 1/2 mod 23
2n = 1 mod 23
2n mod 23 = 1
n = 12
2 * 12 mod 23 == 1

算这么慢，怎么搞，有种标量乘法的计算方式，先做倍数在做加法。假设n=151,对应二进制为10010111

151 = 1*2^7 + 0*2^6 + ...
    = 2^7 + 2^4 + 2^2 + 2^1 + 2^0
151P = 2^7P + 2^4P + 2^2P + 2^1P + 2^0P
  1. 输出密钥对

私钥：dd（标量，保密）。 公钥：Q=dGQ = dG（曲线上的点，公开）。

  1. 加解密过程

选一条椭圆曲线Ep(a,b),并取椭圆曲线上一个点作为基点G, 选定一个大数k作为私钥，并生成公钥Q=nG。 加密：选择随机数r,将消息M生成密文C,密文是一个点对，C=(rG,M+rQ)。 解密：M+rQ-k(rG) = M+r(nG)-n(rG) = M

ECC的核心算法

ECC在非对称加密中的应用主要体现在以下几种算法：

  1. ECDSA（Elliptic Curve Digital Signature Algorithm）

用途：数字签名，用于验证数据的完整性和发送者身份。 流程：

签名生成：

选择私钥 dd 和基点 GG，计算公钥 Q=dGQ = dG。 随机选择一个整数 kk，计算点 R=kGR = kG，取 RR 的横坐标 rr。 计算消息的哈希值 h=Hash(message)h = Hash(message)。 计算签名对 (r,s)(r, s)，其中 s=k−1(h+dr)modns = k^{-1}(h + dr) \mod n，nn 是基点 GG 的阶。

签名验证：

接收者使用发送者的公钥 QQ 和签名 (r,s)(r, s) 验证。 计算 w=s−1modnw = s^{-1} \mod n，然后计算 u1=hwmodnu_1 = hw \mod n 和 u2=rwmodnu_2 = rw \mod n。 计算点 P=u1G+u2QP = u_1G + u_2Q，验证 PP 的横坐标是否等于 rr。

应用：比特币、区块链、SSL/TLS协议中的数字证书签名。

  1. ECDH（Elliptic Curve Diffie-Hellman）

用途：密钥交换，用于在不安全的信道上协商共享密钥。 流程：

通信双方（Alice和Bob）各选择私钥 dAd_A 和 dBd_B，计算公钥 QA=dAGQ_A = d_AG 和 QB=dBGQ_B = d_BG。 双方交换公钥 QAQ_A 和 QBQ_B。 Alice计算共享密钥 S=dAQB=dAdBGS = d_A Q_B = d_A d_B G，Bob计算 S=dBQA=dBdAGS = d_B Q_A = d_B d_A G。 由于 dAQB=dBQAd_A Q_B = d_B Q_A，双方得到相同的共享密钥 SS。

应用：SSL/TLS中的密钥协商、VPN加密。

  1. ECIES（Elliptic Curve Integrated Encryption Scheme）

用途：混合加密，结合ECC和对称加密进行数据加密。

流程：

使用ECDH生成共享密钥。 用共享密钥通过对称加密算法（如AES）加密消息。 使用ECDSA对加密后的数据签名，确保完整性。

应用：安全消息传输、文件加密。

常用椭圆曲线

ECC的安全性和性能依赖于曲线的选择，常见标准曲线包括：

选择曲线的注意事项：

确保曲线参数经过严格验证，避免弱曲线。 使用标准化的曲线（如NIST或Curve25519）以确保安全性和互操作性。

非对称加密解惑

密码学家Lenstra引进了“全球安全（Global Security）”的概念：假设破解一个228字节的RSA秘钥需要的能量少于煮沸一勺水的能量。那么破解一个228字节的椭圆曲线秘钥需要煮沸地球上所有水的能量。如果RSA要达到一个同样的安全水平，你需要一个2,380字节的秘钥。ECC能够使用较小的资源而产生安全性较高的效果。

  1. 非对称加密比对称加密机密性更高吗?

    这个问题无法回答, 机密性高低是根据秘钥长度而变化的

  2. 采用1024bit 秘钥长度的非对称加密, 和采用128bit秘钥长度的对称加密中, 是秘钥更长的非对称加密更安全吗?

    不是。

    非对称加密的密钥长度不能与对称加密的密钥长度进行直接比较。下表是一张密钥长度的比较表（本表摘自《应用密码学》），根据这张表我们可以看出，1024比特的公钥密码与128比特的对称密码相比，反而是128比特的对称密码抵御暴力破解的能力更强。

    对称加密秘钥长度 非对称加密秘钥长度
    128 比特 2304 比特
    112 比特 1792 比特
    80 比特 768 比特
    64 比特 512 比特
    56 比特 384 比特

  3. 有了非对称加密，以后对称加密会被替代吗？

    不会。

    一般来说，在采用具备同等机密性的密钥长度的情况下，非对称加密的处理速度只有对称加密的几百分之一。因此，非对称加密并不适合用来对很长的消息内容进行加密。根据目的的不同，还可能会配合使用对称加密和非对称加密，例如，混合密码系统就是将这两种密码组合而成的。

单向散列函数

“单向散列函数 — 获取消息的指纹”

在刑事侦查中，侦查员会用到指纹。通过将某个特定人物的指纹与犯罪现场遗留的指纹进行对比，就能够知道该人物与案件是否存在关联。

针对计算机所处理的消息，有时候我们也需要用到“指纹”。当需要比较两条消息是否一致时，我们不必直接对比消息本身的内容，只要对比它们的“指纹”就可以了。

本章中，我们将学习单向散列函数的相关知识。使用单向散列函数就可以获取消息的“指纹”，通过对比 “指纹”，就能够知道两条消息是否一致。

下面，我们会先简单介绍一下单向散列函数，并给大家展示具体的例子。然后我们将详细介绍现在使用非常广泛的SHA-I单向散列函数。

root@ser745692301841:/dev_dir/note# md5sum    favicon.ico 
bf487fa2fbf80dcf5d9694e4769065ea  favicon.ico
root@ser745692301841:/dev_dir/note#

什么是单向散列函数

单向散列函数 (one-wayftnction) 有一个输入和一个输出，其中输入称为消息(message)，输出称为散列值(hashvalue)。单向散列函数可以根据消息的内容计算出散列值，而散列值就可以被用来检查消息的完整性。

消息->单向散列函数->散列值

这里的消息不一定是人类能够读懂的文字，也可以是图像文件或者声音文件。单向散列函数不需要知道消息实际代表的含义。无论任何消息，单向散列函数都会将它作为单纯的比特序列来处理，即根据比特序列计算出散列值。

散列值的长度和消息的长度无关。无论消息是1比特，还是100MB，甚至是IOOGB，单向散列函数都会计算出固定长度的散列值。以SHA-I单向散列函数为例，它所计算出的散列值的长度永远是160比特（20字节）。

用户的口令8byte->SHA-1->散列值20byte
扫描仪产生的图像数据512KB->SHA-1->散列值20byte
存储卡中的所有文件4GB->SHA-1->散列值20byte
硬盘中的所有文件80GB->SHA-1->散列值20byte

关于术语

单向散列函数的相关术语有很多变体，不同参考资料中所使用的术语也不同。

单向散列函数也称为 消息摘要函数（message digest function）、哈希函数 或者 杂凑函数。

输人单向散列函数的消息也称为 原像（pre-image）。

单向散列函数输出的散列值也称为 消息摘要（message digest）或者 指纹（fingerprint）。

完整性也称为一致性。

顺便说一句，单向散列函数中的“散列”的英文”hash一词，原意是古法语中的“斧子”，后来被引申为“剁碎的肉末”，也许是用斧子一通乱剁再搅在一起的那种感觉吧。单向散列函数的作用，实际上就是将很长的消息剁碎，然后再混合成固定长度的散列值。

单向散列函数的性质

通过使用单向散列函数，即便是确认几百MB大小的文件的完整性，也只要对比很短的散列值就可以了。那么，单向散列函数必须具备怎样的性质呢？我们来整理一下。

  1. 根据任意长度的消息计算出固定长度的散列值
  2. 能够快速计算出散列值
  3. 消息不同散列值也不同，两个不同的消息产生同一个散列值的情况称为碰撞（collision）
  4. 具备单向性

难以发现碰撞的性质成为抗碰撞(collision resistance)

尽管单向散列函数所产生的散列值是和原来的消息完全不同的比特序列,但是单向散列函数并不是一种加密,因此无法通过解密将散列值还原为原来的消息

单向散列函数的实际应用

下面我们来看一下实际应用单向散列函数的例子。

检测软件是否被篡改

我们可以使用单向散列函数来确认自己下载的软件是否被篡改。

很多软件，尤其是安全相关的软件都会把通过单向散列函数计算出的散列值公布在自己的官方网站上。用户在下载到软件之后，可以自行计算散列值，然后与官方网站上公布的散列值进行对比。通过散列值，用户可以确认自己所下载到的文件与软件作者所提供的文件是否一致。

这样的方法，在可以通过多种途径得到软件的情况下非常有用。为了减轻服务器的压力，很多软件作者都会借助多个网站（镜像站点）来发布软件，在这种情况下，单向散列函数就会在检测软件是否被篡改方面发挥重要作用。

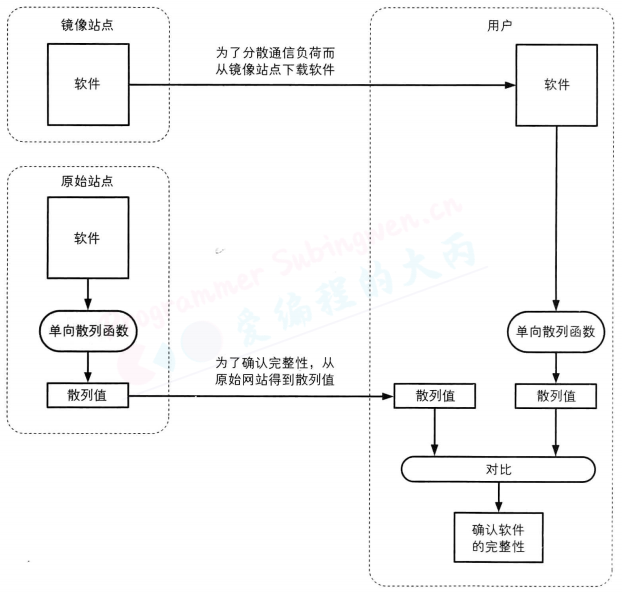
检测软件是否被篡改

消息认证码

使用单向散列函数可以构造消息认证码。

消息认证码是将“发送者和接收者之间的共享密钥”和“消息，进行混合后计算出的散列值。使用消息认证码可以检测并防止通信过程中的错误、篡改以及伪装。

消息认证码在SSL/TLS中也得到了运用，关于SSL/TLS我们将后边章节中介绍。

数字签名

在进行数字签名时也会使用单向散列函数。

数字签名是现实社会中的签名（sign）和盖章这样的行为在数字世界中的实现。数字签名的处理过程非常耗时，因此一般不会对整个消息内容直接施加数字签名，而是先通过单向散列函数计算出消息的散列值，然后再对这个散列值施加数字签名。

伪随机数生成器

使用单向散列函数可以构造伪随机数生成器。

密码技术中所使用的随机数需要具备“事实上不可能根据过去的随机数列预测未来的随机数列”这样的性质。为了保证不可预测性，可以利用单向散列函数的单向性。

一次性口令

使用单向散列函数可以构造一次性口令（one-time password）。

一次性口令经常被用于服务器对客户端的合法性认证。在这种方式中，通过使用单向散列函数可以保证口令只在通信链路上传送一次（one-time），因此即使窃听者窃取了口令，也无法使用。

MD4、MD5

MD4是由Rivest于1990年设计的单向散列函数，能够产生128比特的散列值（RFC1186，修订版RFC1320）。不过，随着Dobbertin提出寻找MD4散列碰撞的方法，因此现在它已经不安全了。

MD5是由Rwest于1991年设计的单项散列函数，能够产生128比特的散列值（RFC1321）。

MD5的强抗碰撞性已经被攻破，也就是说，现在已经能够产生具备相同散列值的两条不同的消息，因此它也已经不安全了。

MD4和MD5中的MD是消息摘要（Message Digest）的缩写。

计算Md5的方式1

package main

import (
    "crypto/md5"
    "encoding/hex"
    "fmt"
)

func getMD5_1(str []byte) string {
    // 计算数据的md5
    result := md5.Sum(str)
    fmt.Println(result)
    fmt.Printf("%x\n", result)
    // 数据格式化16进制格式字符串
    res := fmt.Sprintf("%x", result)
    fmt.Println(res)
    // 这是另一种格式化切片的方式
    res = hex.EncodeToString(result[:])
    fmt.Println("res: ", res)
    return res
}

func main() {
    str := "hello world"
    getMD5_1([]byte(str))
}

// root@ser745692301841:/dev_dir/note/testcode# go run main.go
// [94 182 59 187 224 30 238 208 147 203 34 187 143 90 205 195]
// 5eb63bbbe01eeed093cb22bb8f5acdc3
// 5eb63bbbe01eeed093cb22bb8f5acdc3
// res:  5eb63bbbe01eeed093cb22bb8f5acdc3

计算Md5的方式2

package main

import (
    "crypto/md5"
    "encoding/hex"
    "fmt"
    "io"
)

func getMD5_2(str []byte) string {
    // 创建一个使用MD5校验的Hash对象
    myHash := md5.New()
    // 通过io操作将数据写入hash对象中
    io.WriteString(myHash, "hello")
    // io.WriteString(myHash, " world")
    myHash.Write([]byte(" world"))

    // 计算结果
    result := myHash.Sum(nil)
    fmt.Println(result)

    // 将结果转换为16进制格式字符串
    res := fmt.Sprintf("%x", result)
    fmt.Println(res)

    // 这是另外一种格式化切片的方式
    res = hex.EncodeToString(result)
    fmt.Println(res)

    return res
}

func main() {
    str := "hello world"
    getMD5_2([]byte(str))
}

// root@ser745692301841:/dev_dir/note/testcode# go run main.go
// [94 182 59 187 224 30 238 208 147 203 34 187 143 90 205 195]
// 5eb63bbbe01eeed093cb22bb8f5acdc3
// 5eb63bbbe01eeed093cb22bb8f5acdc3

SHA-1、SHA-224、SHA-256、SHA-384、SHA-512

SHA-1是由NIST（NationalInstituteOfStandardsandTechnology，美国国家标准技术研究所）设计的一种能够产生160比特的散列值的单向散列函数。1993年被作为美国联邦信息处理标准规格（FIPS PUB 180）发布的是SHA,1995年发布的修订版FIPS PUB 180-1称为SHA-1。

SHA-1的消息长度存在上限，但这个值接近于264比特，是个非常巨大的数值，因此在实际应用中没有问题。

SHA-256、SHA-384和SHA-512都是由NIST设计的单向散列函数，它们的散列值长度分别为256比特、384比特和512比特。这些单向散列函数合起来统称SHA-2，它们的消息长度也存在上限（SHA-256的上限接近于 264 比特，SHA-384 和 SHA-512的上限接近于 2128 比特）。这些单向散列函数是于2002年和 SHA-1 一起作为 FIPS PUB 180-2发布的 SHA-1 的强抗碰撞性已于2005年被攻破, 也就是说，现在已经能够产生具备相同散列值的两条不同的消息。不过，SHA-2还尚未被攻破。

比特数 字节数
MD4 128bit 16byte
MD5 128bit 16byte
SHA-1 160bit 20byte
SHA-224 224bit 28byte
SHA-256 256bit 32byte
SHA-384 384bit 48byte
SHA-512 512bit 64byte 
package main

import (
    "crypto/sha256"
    "encoding/hex"
    "fmt"
    "io"
    "os"
)

func getSha256(str []byte) string {
    fp, err := os.Open(string(str))
    if err != nil {
        return "文件打开失败"
    }

    // 创建基于sha256算法的Hash对象
    myHash := sha256.New()
    // 将文件数据拷贝给哈希函数
    num, err := io.Copy(myHash, fp)
    if err != nil {
        return "拷贝文件失败"
    }
    fmt.Println("文件大小：", num)
    // 计算文件的哈希值
    tmp1 := myHash.Sum(nil)
    // 数据格式转换
    result := hex.EncodeToString(tmp1)
    fmt.Println("sha256: ", result)
    return result
}

func main() {
    str := "./private.pem"
    getSha256([]byte(str))
}

// root@ser745692301841:/dev_dir/note/testcode# go run main.go
// 文件大小： 302
// sha256:  f47b74aaddbdf8e1b940f4be19eb17e3e5227439c45da0bd41e35b1dc93cd15b

消息认证码

“消息认证码 — 消息被正确传送了吗？”

Alice和Bob的故事

像以前一样，我们还是从一个Alice和Bob的故事开始讲起。不过，这一次Alice和Bob分别是两家银行，Alice银行通过网络向Bob银行发送了一条汇款请求，Bob银行收到的请求内容是：

从 账户A-5374 向 账户B-6671 汇款 1000万元

当然，Bob银行所收到的汇款请求内容必须与Alice银行所发送的内容是完全一致的。如果主动攻击者Mallory在中途将Alice银行发送的汇款请求进行了篡改，那么Bob银行就必须要能够识别出这种篡改，否则如果Mallory将收款账户改成了自己的账户，那么1000万元就会被盗走。

话说回来，这条汇款请求到底是不是Alice银行发送的呢？有可能Alice银行根本就没有发送过汇款请求，而是由主动攻击者Mallory伪装成Alice银行发送的。如果汇款请求不是来自Alice银行，那么就绝对不能执行汇款。

现在我们需要关注的问题是汇款请求（消息）的 “完整性” 和 “认证” 这两个性质。

消息的完整性(integrity), 指的是“消息没有被篡改”这一性质，完整性也叫一致性 。如果能够确认汇款请求的内容与Alice银行所发出的内容完全一致，就相当于是确认了消息的完整性，也就意味着消息没有被篡改。

消息的认证（authentication）指的是“消息来自正确的发送者”这一性质。如果能够确认汇款请求确实来自Alice银行，就相当于对消息进行了认证，也就意味着消息不是其他人伪装成发送者所发出的。

通过使用本章中要介绍的消息认证码，我们就可以同时识别出篡改和伪装，也就是既可以确认消息的完整性，也可以进行认证。

什么是消息认证码

消息认证码（message authentication code） 是一种确认完整性并进行认证的技术，取三个单词的首字母，简称为MAC。

消息认证码的输入包括任意长度的消息和一个发送者与接收者之间共享的密钥，它可以输出固定长度的数据，这个数据称为MAC值。

单向散列函数与消息认证码的比较

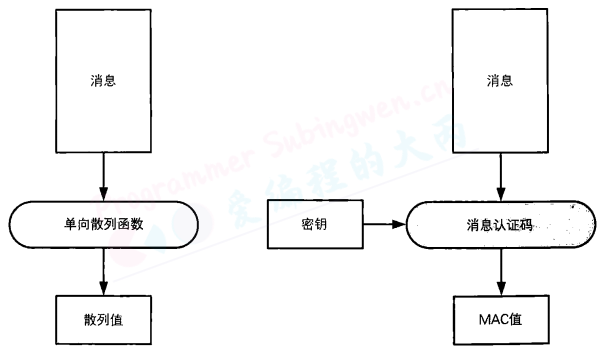
单向散列函数与消息认证码的比较

消息认证码的使用步骤

“我们还是以Alice银行和Bob银行的故事为例，来讲解一下消息认证码的使用步骤”：

消息认证码的使用步骤
  1. 发送者Alice与接收者Bob事先共享密钥。
  2. 发送者Alice根据汇款请求消息计算MAC值（使用共享密钥）。
  3. 发送者Alice将汇款请求消息和MAC值两者发送给接收者Bob。
  4. 接收者Bob根据接收到的汇款请求消息计算MAC值（使用共享密钥）。
  5. 接收者Bob将自己计算的MAC值与从Alice处收到的MAC值进行对比。
  6. 如果两个MAC值一致，则接收者Bob就可以断定汇款请求的确来自Alice（认证成功）；如果不一致，则可以断定消息不是来自Alice（认证失败）。

HMAC介绍

HMAC是一种使用单向散列函数来构造消息认证码的方法（RFC2104），其中HMAC的H就是Hash的意思。

HMAC中所使用的单向散列函数并不仅限于一种，任何高强度的单向散列函数都可以被用于HMAC,如果将来设计出新的单向散列函数，也同样可以使用。

使用SHA-I、MD5、RIPEMD-160所构造的HMAC，分别称为HMAC-SHA-1、HMAC-MD5和HMAC-RlPEMD。

使用HMAC通过秘钥将消息生成消息认证码的内部实现：

使用HMAC通过秘钥将消息生成消息认证码的内部实现

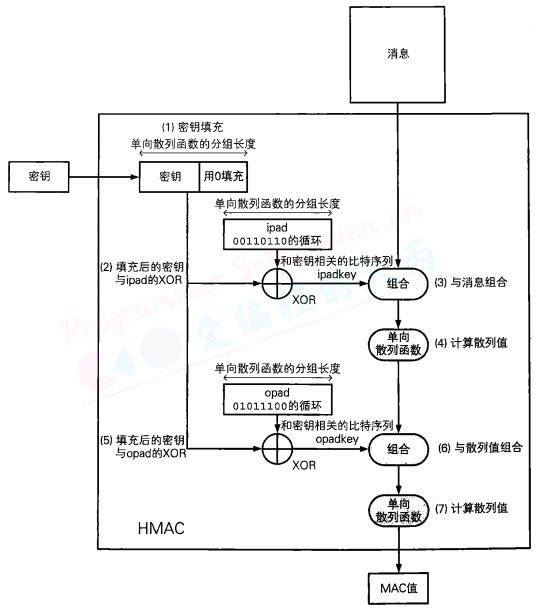
通过上述流程我们可以看出，最后得到的MAC值，一定是一个和输入的消息以及密钥都相关的长度固定的比特序列。

Go中对HMAC的使用

package main

import (
    "crypto/hmac"
    "crypto/sha256"
    "fmt"
)

// 生成消息认证码
func GenerateHMAC(src, key []byte) []byte {
    // 创建一个底层采用sha256算法的 hash.Hash 接口
    myHmac := hmac.New(sha256.New, key)
    // md5.New、sha1.New、sha256.New、sha256.New224
    // sha512.New、sha512.New384
    // 参数 key: 和数据进行混合运算使用的秘钥

    // 添加测试数据
    myHmac.Write(src)

    // 计算结果
    result := myHmac.Sum(nil)
    return result
}

// 验证消息认证码
func VerifyHMAC(res, src, key []byte) bool {
    // 创建一个底层采用sha256算法的 hash.Hash 接口
    myHmac := hmac.New(sha256.New, key)
    // 添加测试数据
    myHmac.Write(src)
    // 计算结果
    result := myHmac.Sum(nil)
    // 比较结果
    return hmac.Equal(res, result)
}

func main() {
    key := []byte("我是消息认证码秘钥")
    src := []byte("我是消息认证码测试数据")
    result := GenerateHMAC(src, key)
    final := VerifyHMAC(result, src, key)
    if final {
        fmt.Println("消息认证码认证成功!!!")
    } else {
        fmt.Println("消息认证码认证失败 ......")
    }
}

消息认证码的密钥配送问题

在消息认证码中，需要发送者和接收者之间共享密钥，而这个密钥不能被主动攻击者Mallory获取。如果这个密钥落入Mallory手中，则Mallory也可以计算出MAC值，从而就能够自由地进行篡改和伪装攻击，这样一来消息认证码就无法发挥作用了。

发送者和接收者需要共享密钥，这一点和我们介绍的对称加密很相似。实际上，对称加密的密钥配送问题在消息认证码中也同样会发生。关于秘钥的配送后边章节会介绍如何使用非对称加密的方式进行解决。

消息认证码无法解决的问题

假设发送者Alice要向接收者Bob发送消息，如果使用了消息认证码，接收者Bob就能够断定自己收到的消息与发送者Alice所发出的消息是一致的，这是因为消息中的MAC值只有用Alice和Bob之间共享的密钥才能够计算出来，即便主动攻击者Mallory篡改消息，或者伪装成Alice发送消息，Bob也能够识别出消息的篡改和伪装。

但是，消息认证码也不能解决所有的问题，例如“对第三方证明”和“防止否认”，这两个问题就无法通过消息认证码来解决。下面我们来逐一解释一下。

对第三方认证

假设Bob在接收了来自Alice的消息之后，想要向第三方验证者Victor证明这条消息的确是Alice发送的，但是用消息认证码无法进行这样的证明，这是为什么呢？

首先，Victor要校验MAC值，就需要知道Alice和Bob之间共享的密钥。

假设Bob相信Victor, 同意将密钥告诉Victor,即便如此，Victor也无法判断这条消息是由Alice发送的，因为Victor可以认为：“即使MAC值是正确的，发送这条消息的人也不一定是Alice，还有可能是Bob。”

能够计算出正确MAC值的人只有Alice和Bob，在他们两个人之间进行通信时，可以断定是对方计算了MAC值，这是因为共享这个密钥的双方之中，有一方就是自己。然而，对于第三方Victor、Alice或Bob却无法证明是对方计算了MAC值，而不是自己。

使用第7章中将要介绍的数字签名就可以实现对第三方的证明。

防止否认

假设Bob收到了包含MAC值的消息，这个MAC值是用Alice和Bob共享的密钥计算出来的，因此Bob能够判断这条消息的确来自Alice。

但是，上面我们讲过，Bob无法向验证者Victor证明这一点，也就是说，发送者Alice可以向Victor声称：“我没有向Bob发送过这条消息。”这样的行为就称为否认（repudiation）。

Alice可以说“这条消息是Bob自己编的吧”，“说不定Bob的密钥被主动攻击者Mallory给盗取了，我的密钥可是妥善保管着呢” 等。说白了，就是Alice和Bob吵起来了。

即便Bob拿MAC值来举证，Victor也无法判断Alice和Bob谁的主张才是正确的，也就是说，用消息认证码无法防止否认（nonrepudiatlon） 。

消息认证码总结

消息认证码是对消息进行认证并确认其完整性的技术。通过使用发送者和接收者之间共享的密钥，就可以识别出是否存在伪装和篡改行为。

消息认证码可以使用单向散列函数HMAC， 对称加密也可以实现， 这里不再进行介绍。

消息认证码中，由于发送者和接收者共享相同的密钥，因此会产生无法对第三方证明以及无法防止否认等问题。在下一章中，我们将介绍能够解决这些问题的数字签名。

数字签名

“数字签名 — 消息到底是谁写的”

本章中我们将学习数字签名的相关知识。数字签名是一种将相当于现实世界中的盖章、签字的功能在计算机世界中进行实现的技术。使用数字签名可以识别篡改和伪装，还可以防止否认。

从消息认证到数字签名

消息认证码的局限性

通过使用第6章中介绍的消息认证码，我们可以识别消息是否被篡改或者发送者身份是否被伪装，也就是可以校验消息的完整性，还可以对消息进行认证。然而，比如在出具借条的场景中却无法使用消息认证码，因为消息认证码无法防止否认。

消息认证码之所以无法防止否认，是因为消息认证码需要在发送者Alice和接收者Bob两者之间共享同一个密钥。正是因为密钥是共享的，所以能够使用消息认证码计算出正确MAC值的并不只有发送者Alice，接收者Bob也可以计算出正确的MAC值。由于Alice和Bob双方都能够计算出正确的MAC值，因此对于第三方来说，我们无法证明这条消息的确是由Alice生成的。

通过数字签名解决问题

下面请大家开动一下脑筋。假设发送者Alice和接收者Bob不需要共享一个密钥，也就是说，Alice和Bob各自使用不同的密钥。

我们假设Alice使用的密钥是一个只有Alice自己才知道的私钥。当Alice发送消息时，她用私钥生成一个“签名”。相对地，接收者Bob则使用一个和Alice不同的密钥对签名进行验证。使用Bob的密钥无法根据消息生成签名，但是用Bob的密钥却可以对Alice所计算的签名进行验证，也就是说可以知道这个签名是否是通过Alice的密钥计算出来的。如果真有这么一种方法的话，那么不管是识别篡改、伪装还是防止否认就都可以实现了吧 ？

实际上，这种看似很神奇的技术早就已经问世了，这就是 数字签名（digital signat.ure）。

签名的生成和验证

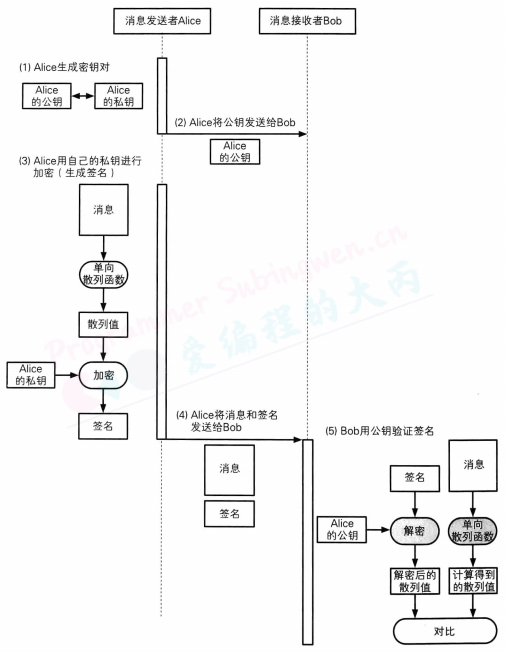
在数字签名技术中，出现了下面两种行为：

生成消息签名 这一行为是由消息的发送者Alice来完成的，也称为“对消息签名”。生成签名就是根据消息内容计算数字签名的值，这个行为意味着 “我认可该消息的内容”。

验证数字签名 这一行为一般是由消息的接收者Bob来完成的，但也可以由需要验证消息的第三方来完成，这里的第三方我们暂且将其命名为验证者Victor。验证签名就是检查该消息的签名是否真的属于Alice，验证的结果可以是成功或者失败，成功就意味着这个签名是属于Alice的，失败则意味着这个签名不是属于Alice的。

在数字签名中，生成签名和验证签名这两个行为需要使用各自专用的密钥来完成。

Alice使用“签名密钥”来生成消息的签名，而Bob和Victor则使用“验证密钥”来验证消息的签名。数字签名对签名密钥和验证密钥进行了区分，使用验证密钥是无法生成签名的。这一点非常重要。此外，签名密钥只能由签名的人持有 ，而 验证密钥则是任何需要验证签名的人都可以持有。

刚才讲的这部分内容，是不是觉得似曾相识呢？

没错，这就是我们讲过的非对称加密。公钥密码和上面讲的数字签名的结构非常相似。在非对称加密中，密钥分为加密密钥和解密密钥，用加密密钥无法进行解密。此外，解密密钥只能由需要解密的人持有，而加密密钥则是任何需要加密的人都可以持有。你看，数字签名和非对称加密是不是很像呢？

实际上，数字签名和非对称加密有着非常紧密的联系，简而言之，数字签名就是通过将非对称加密 “反过来用” 而实现的。下面我们来将密钥的使用方式总结成一张表：

私钥 公钥
非对称加密 接收者解密时使用 发送者加密时使用
数字签名 签名者生成签名时使用 验证者验证签名时使用
谁持有密钥 个人持有 只要需要，任何人都可以持有

非对称加密和数字签名

下面我们再来详细讲一讲非对称加密与数字签名之间的关系。

要实现数字签名，我们可以使用第4章中介绍的非对称加密。非对称加密包括一个由公钥和私钥组成的密钥对，其中公钥用于加密，私钥用于解密。

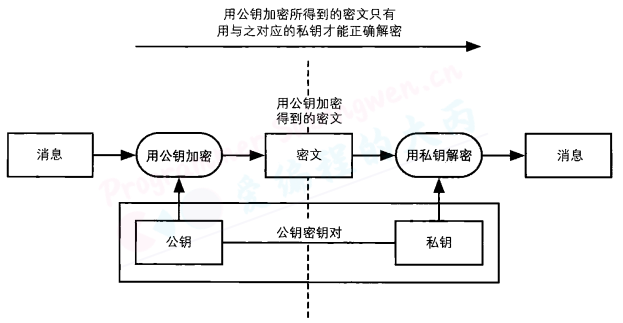
非对称加密

数字签名中也同样会使用公钥和私钥组成的密钥对，不过这两个密钥的用法和非对称加密是相反的，即用私钥加密相当于生成签名，而用公钥解密则相当于验证签名。请大家通过比较两张图示来理解一下“反过来用”到底是什么样的情形。

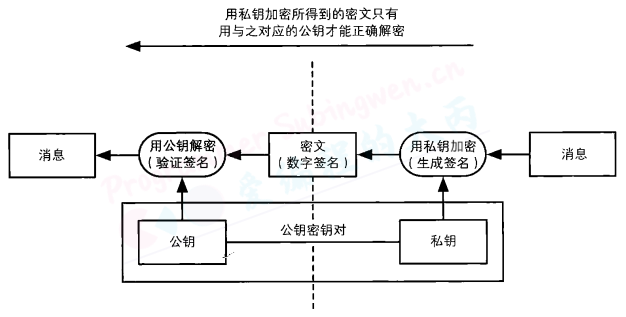
数字签名过程

那么为什么加密相当于生成签名，而解密相当于验证签名呢？要理解这个问题，我们需要回想一下非对称加密中讲过的知识，即组成密钥对的两个密钥之间存在严密的数学关系，它们是一对无法拆散的伙伴。

用公钥加密所得到的密文，只能用与该公钥配对的私钥才能解密：同样地，用私钥加密所得到的密文，也只能用与该私钥配对的公钥才能解密。也就是说，如果用某个公钥成功解密了密文，那么就能够证明这段密文是用与该公钥配对的私钥进行加密所得到的。

用私钥进行加密这一行为只能由持有私钥的人完成，正是基于这一事实，我们才可以将用私钥加密的密文作为签名来对待。

由于公钥是对外公开的，因此任何人都能够用公钥进行解密，这就产生了一个很大的好处，即任何人都能够对签名进行验证。

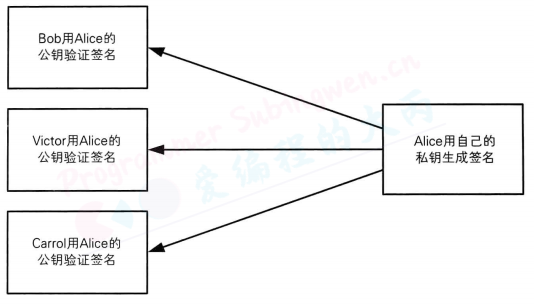
用Alice的公钥验证签名

数字签名的方法

下面我们来具体介绍两种生成和验证数字签名的方法。

  1. 直接对消息签名的方法
  2. 对消息的散列值签名的方法

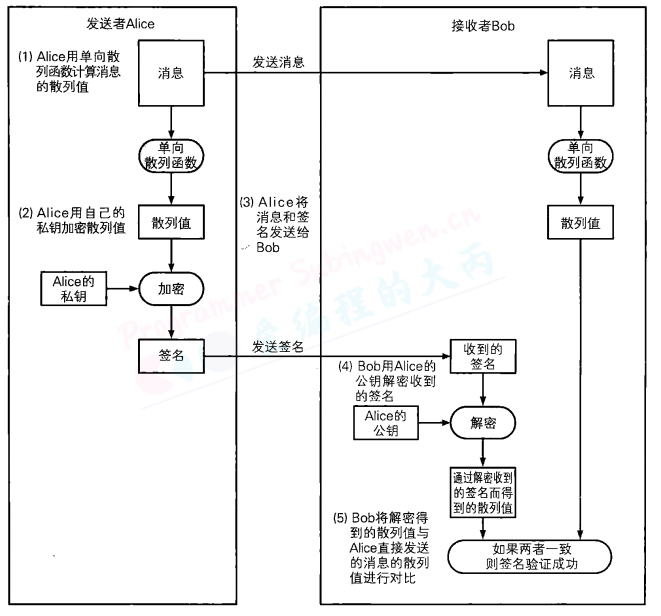
直接对消息签名的方法比较容易理解，但实际上并不会使用；对消息的散列值签名的方法稍微复杂一点，但实际中我们一般都使用这种方法。

使用直接对消息签名的方法，需要对整个消息进行加密，非常耗时，这是因为非对称加密算法本来就非常慢。那么，我们能不能生成一条很短的数据来代替消息本身呢？这就是单向散列函数。

于是我们不必再对整个消息进行加密（即对消息签名），而是只要先用单向散列函数求出消息的散列值，然后再将散列值进行加密（对散列值签名）就可以了。无论消息有多长，散列值永远都是这么短，因此对其进行加密（签名）是非常轻松的。

  1. Alice用单向散列函数计算消息的散列值
  2. Alice用自己的私钥对散列值进行加密
  3. Alice将消息和签名发送给Bob
  4. Bob用Alice的公钥对收到的签名进行解密
  5. Bob将签名解密后得到的散列值与Alice直接发送的消息的散列值进行对比

​ 用私钥加密散列值所得到的密文就是Alice对这条散列值的签名，由于只有Alice才持有自己的私钥因此,​ 除了Alice以外，其他人是无法生成相同的签名（密文）的。

如果收到的签名确实是用Alice的私钥进行加密而得到的密文（签名），那么用Alice的公钥应该能够正确解密，解密的结果应该等于消息的散列值。如果收到的签名不是用Alice的私钥进行加密而得到的密文，那么就无法用Alice的公钥正确解密（解密后得到的数据看起来是随机的）。

如果两者一致，则签名验证成功；如果两者不一致，则签名验证失败。我们将数字签名中生成签名和验证签名的过程整理成一张时间流程图 。

Alice对消息的散列值签名，Bob验证签名

Alice对消息的散列值签名, Bob验证签名
Alice对消息的散列值签名，Bob验证签名按时间顺序

通过RSA实现数字签名

前边章节已经介绍过如何通过自己编写的go代码生成非对称加密算法RSA的公钥和私钥文件，假设公钥文件的文件名为 public.pem ，私钥文件对应的文件名为 private.pem。

生成与验证数字签名

package main

import (
    "crypto"
    "crypto/rand"
    "crypto/rsa"
    "crypto/sha256"
    "crypto/x509"
    "encoding/pem"
    "errors"
    "fmt"
    "os"
)

// 生成数字签名
func SignatureRSA() ([]byte, error) {
    // 从私钥中读生成的私钥内容
    fp, err := os.Open("private.pem")
    if err != nil {
        return nil, errors.New("打开私钥文件 - private.pem 失败")
    }
    defer fp.Close()
    // 读文件内容
    fileInfo, _ := fp.Stat()
    all := make([]byte, fileInfo.Size())
    _, err = fp.Read(all)
    if err != nil {
        return nil, errors.New("读文件内容失败")
    }
    fmt.Println("文件内容: ", string(all))

    // 将数据解析为pem格式的数据块
    block, _ := pem.Decode(all)

    // 解析pem数据块，得到私钥
    key, err := x509.ParsePKCS8PrivateKey(block.Bytes)
    if err != nil {
        fmt.Println(err)
        return nil, errors.New("解析私钥失败!")
    }
    priv_Key := key.(*rsa.PrivateKey)

    // 待签名数据
    myData := []byte("hello world")

    // 将数据通过哈希函数生成信息摘要
    myHash := sha256.New()
    myHash.Write(myData)
    result := myHash.Sum(nil)

    // 生成签名
    mySignature, err := rsa.SignPKCS1v15(rand.Reader, priv_Key, crypto.SHA256, result)
    if err != nil {
        fmt.Println(err)
        return nil, errors.New("生成签名失败")
    }

    return mySignature, nil
}

// 验证数字签名
func VerifyRSA(src []byte) error {
    // 从公钥文件中读生成的公钥内容
    fp, err := os.Open("public.pem")
    if err != nil {
        return errors.New("打开公钥文件 - public.pem 失败")
    }
    defer fp.Close()

    // 读文件内容
    fileInfo, _ := fp.Stat()
    all := make([]byte, fileInfo.Size())
    num, err := fp.Read(all)
    if err != nil {
        return errors.New("读文件内容失败")
    }
    fmt.Println("文件大小: ", num)

    // 将公钥数据解析为Pem格式的数据块
    block, _ := pem.Decode(all)
    // 将公钥从pem数据块中提取出来
    pubInterface, err := x509.ParsePKIXPublicKey(block.Bytes)
    if err != nil {
        return errors.New("解析公钥失败!!!")
    }
    // 公钥接口转为公钥对象
    pubKey := pubInterface.(*rsa.PublicKey)
    // 待认证的数据
    myData := []byte("hello world")
    // 将数据通过哈希函数生成信息摘要
    myHash := sha256.New()
    myHash.Write(myData)
    result := myHash.Sum(nil)

    // 数据认证
    err = rsa.VerifyPKCS1v15(pubKey, crypto.SHA256, result, src)
    if err != nil {
        return err
    }

    fmt.Println("数字签名验证成功")
    return nil
}

// root@ser745692301841:/dev_dir/note/testcode# openssl genrsa -out private.pem 2048
// root@ser745692301841:/dev_dir/note/testcode# openssl rsa -in private.pem -pubout -out public.pem
// writing RSA key

func main() {
    signature, err := SignatureRSA()
    if err != nil {
        fmt.Println(err.Error())
        panic(err)
    }
    err = VerifyRSA(signature)
    if err != nil {
        fmt.Println(err.Error())
        panic(err)
    }
}

数字签名无法解决的问题

用数字签名既可以识别出篡改和伪装，还可以防止否认。也就是说，我们同时实现了确认消息的完整性、进行认证以及否认防止。现代社会中的计算机通信从这一技术中获益匪浅。

然而，要正确使用数字签名，有一个大前提，那是用于验证签名的公钥必须属于真正的发送者 。即便数字签名算法再强大，如果你得到的公钥是伪造的，那么数字签名也会完全失效。

现在我们发现自己陷人了一个死循环一一一数字签名是用来识别消息篡改、伪装以及否认的，但是为此我们又必须从没有被伪装的发送者得到没有被篡改的公钥才行。

为了能够确认自己得到的公钥是否合法，我们需要使用证书。所谓证书，就是将公钥当作一条消息，由一个可信的第三方对其签名后所得到的公钥。

当然，这样的方法只是把问题转移了而已。为了对证书上施加的数字签名进行验证，我们必定需要另一个公钥，那么如何才能构筑一个可信的数字签名链条呢？又由谁来颁发可信的证书呢？到这一步，我们就已经踏人了社会学的领域。我们需要让公钥以及数字签名技术成为一种社会性的基础设施，即公钥基础设施（Public Key Intrastructure），简称PKI. 关于证书和PKI我们将在第8章中介绍。

数字签名无法解决的问题

证书

证书的应用场景

证书标准规范X.509

证书规范

证书格式

CA证书

公钥基础设施PKI

什么是公钥基础设施

PKI的组成要素

用户

认证机构CA

仓库

各种各样的PKI

SSL/TLS

客户端与服务器

用SSL/TLS承载HTTP

HTTPS

HTTP和HTTPS

HTTPS优缺点